Chaos in high-dimensional dissipative dynamical systems

Abstract

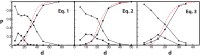
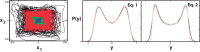
For dissipative dynamical systems described by a system of ordinary differential equations, we address the question of how the probability of chaotic dynamics increases with the dimensionality of the phase space. We find that for a system of d globally coupled ODE's with quadratic and cubic non-linearities with randomly chosen coefficients and initial conditions, the probability of a trajectory to be chaotic increases universally from ~10(-5)- 10(-4) for d = 3 to essentially one for d ~ 50. In the limit of large d, the invariant measure of the dynamical systems exhibits universal scaling that depends on the degree of non-linearity, but not on the choice of coefficients, and the largest Lyapunov exponent converges to a universal scaling limit. Using statistical arguments, we provide analytical explanations for the observed scaling, universality, and for the probability of chaos.

Figure 1. Numerically measured probability of different types of dynamics as a function of dimension d of the phase space for Eq. (1)

(left panel), Eq. (2) (central panel), Eq. (3) (right panel): • - chaotic trajectories, ■ - limit cycles, ▲ - stable fixed points. For each case, the theoretical estimate for the probability of chaotic trajectories (see main text) is shown by a dashed line (red color online).

Figure 2. Scaling of the size of chaotic trajectories.

Left panel: Examples of x₁, x₂ projections of trajectories for the dynamics described by (3) for d = 10 (blue), d = 15 (green), d = 30 (red), and d = 45(black), illustrating the scaling x_i ~ d^3/2. Central panel: The probability density for the scaled coordinate P(y) vs. y = x/d^α, α = 1 of the solution of Eq. (1) for d = 150 (solid black line), d = 100 (dashed red line), and the histogram of the solution of (10) (thick grey line). Right panel: The probability density for the scaled coordinate P(y) vs. y = x/d^α, α = 3/4 of the solution of Eq. (2) for d = 65 (solid black line), d = 50 (dashed red line), and the histogram of the solution of (10) (thick grey line).

Figure 3. The scaled LLE λ/d^β as a function of the dimension d of phase space for (1);

β = 2, black circle; (2), β = 3, square, shifted to the right, red online; and (3), triangle, shifted to the left, blue online, β = 9/2. For large d, the LLE for (1) extrapolates to λ/d^β → λ^* ≈ 0.235. (see main text).