MRI reconstruction of multi-image acquisitions using a rank regularizer with data reordering

Abstract

Purpose: To improve rank constrained reconstructions for undersampled multi-image MRI acquisitions.

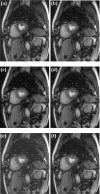
Methods: Motivated by the recent developments in low-rank matrix completion theory and its applicability to rapid dynamic MRI, a new reordering-based rank constrained reconstruction of undersampled multi-image data that uses prior image information is proposed. Instead of directly minimizing the nuclear norm of a matrix of estimated images, the nuclear norm of reordered matrix values is minimized. The reordering is based on the prior image estimates. The method is tested on brain diffusion imaging data and dynamic contrast enhanced myocardial perfusion data.

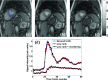
Results: Good quality images from data undersampled by a factor of three for diffusion imaging and by a factor of 3.5 for dynamic cardiac perfusion imaging with respiratory motion were obtained. Reordering gave visually improved image quality over standard nuclear norm minimization reconstructions. Root mean squared errors with respect to ground truth images were improved by ∼18% and ∼16% with reordering for diffusion and perfusion applications, respectively.

Conclusions: The reordered low-rank constraint is a way to inject prior image information that offers improvements over a standard low-rank constraint for undersampled multi-image MRI reconstructions.

FIG. 1.

Illustration of nuclear norm reduction with reordering. Plots of nuclear norms for randomly generated complex matrices without and with reordering. Corresponding zoomed regions of the plots are also shown.

FIG. 2.

Nuclear norm reduction in actual scanner data. Plot of singular values of image matrix obtained from (a) a fully sampled diffusion imaging dataset with 64 directions and (b) a fully sampled perfusion dataset with 80 time frames. Nuclear norms (NNs) without and with reordering are also shown. Corresponding zoomed versions are also shown.

FIG. 3.

Determining optimal reordering of columns using Casorati matrix from a cardiac perfusion dataset. (a) Comparison of nuclear norms (i) without any reordering (labeled original norm) with (ii) reordering all columns in an ascending fashion (labeled all columns ascend) and with (iii) reordering only a random subset of columns in ascending fashion while the remaining columns reordered in descending fashion for 100 000 experiments. (b) Comparison of nuclear norms with different ascending/descending reordering combinations for real and imaginary parts to determine optimal reordering within each column.

FIG. 4.

Illustration of rank constrained reconstruction with perfect reordering. (a) Fully sampled data with IFT reconstruction. One diffusion encoding direction is shown. (b) Corresponding R = 4 IFT reconstruction. (c) Corresponding R = 4 standard low-rank reconstruction. (d) Corresponding R = 4 low-rank reconstruction with reordering. [(e)–(h)] Same as [(a)–(d)] but for a time frame in a perfusion dataset.

FIG. 5.

Comparison of diffusion imaging reconstructions. (a) Ground truth image for a diffusion direction reconstructed using inverse Fourier transform from fully sampled k-space data. [(b) and (c)] Corresponding R = 3 rank constrained reconstructions without and with reordering, respectively. [(d) and (e)] Absolute difference images between (a) and (b) and between (a) and (c), respectively.

FIG. 6.

Comparison of perfusion imaging reconstructions—spatial and temporal characteristics. (a) Ground truth postcontrast image reconstructed using inverse Fourier transform from fully sampled k-space data. ROIs are shown in the myocardium and left ventricular blood pool. Corresponding R = 3.5 reconstruction with standard rank constraint (b) and with reordered rank constraint (c). (d) Mean intensity time curves from the blood pool and myocardium ROIs.

FIG. 7.

Monte Carlo simulations using random matrices of smaller sizes to determine if reordering increases the nuclear norm. (a) Map in which color represents the fraction of the number of times (out of 100 000 randomly generated complex matrices of a fixed size) reordering resulted in a nuclear norm that was equal to or greater than the nuclear norm of the original matrix. The size of the matrix is given by the x and y coordinates of the location. (b) Detail of the top left corner of the map for low values of N and M.

FIG. 8.

Reconstruction sensitivity to prior image quality. (a) Ground truth fully sampled time frame reconstructed using IFT. (b) Reordered rank constrained reconstruction with prior estimated using spatiotemporal TV reconstruction [Eq. (3)]. (c) Overly smoothed version of the STCR prior obtained with a spatial total variation filter. (d) Reordered rank constrained reconstruction using the smoothed STCR prior in (c). (e) Noisy version of STCR prior obtained by adding complex random Gaussian noise. (f) Reordered rank constrained reconstructions using noisy STCR prior in (e).

FIG. 9.

Reconstruction sensitivity to reconstruction parameter τ. (a) Low-rank reconstruction with optimal τ value. Corresponding image with τ scaled up by a factor of five (b) and scaled down by a factor of five (c). [(d)–(f)] Same as [(a)–(c)] but with reordered rank constraint.

FIG. 10.

Normalized reconstruction error plot for different undersampling factors without any reordering (labeled “low rank”) and with estimated and perfect reordering for (a) diffusion imaging and (b) perfusion imaging data.