Subject-specific computational modeling of DBS in the PPTg area

Abstract

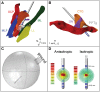
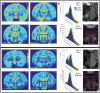
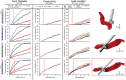
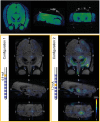
Deep brain stimulation (DBS) in the pedunculopontine tegmental nucleus (PPTg) has been proposed to alleviate medically intractable gait difficulties associated with Parkinson's disease. Clinical trials have shown somewhat variable outcomes, stemming in part from surgical targeting variability, modulating fiber pathways implicated in side effects, and a general lack of mechanistic understanding of DBS in this brain region. Subject-specific computational models of DBS are a promising tool to investigate the underlying therapy and side effects. In this study, a parkinsonian rhesus macaque was implanted unilaterally with an 8-contact DBS lead in the PPTg region. Fiber tracts adjacent to PPTg, including the oculomotor nerve, central tegmental tract, and superior cerebellar peduncle, were reconstructed from a combination of pre-implant 7T MRI, post-implant CT, and post-mortem histology. These structures were populated with axon models and coupled with a finite element model simulating the voltage distribution in the surrounding neural tissue during stimulation. This study introduces two empirical approaches to evaluate model parameters. First, incremental monopolar cathodic stimulation (20 Hz, 90 μs pulse width) was evaluated for each electrode, during which a right eyelid flutter was observed at the proximal four contacts (-1.0 to -1.4 mA). These current amplitudes followed closely with model predicted activation of the oculomotor nerve when assuming an anisotropic conduction medium. Second, PET imaging was collected OFF-DBS and twice during DBS (two different contacts), which supported the model predicted activation of the central tegmental tract and superior cerebellar peduncle. Together, subject-specific models provide a framework to more precisely predict pathways modulated by DBS.

Keywords: Parkinson's disease; deep brain stimulation; diffusion tensor; finite element; non-human primate; pedunculopontine nucleus.

Figure 1

Model geometry and FEM. (A) The geometry of the fiber pathways in the PPTg area in relation to the DBS lead location. CTG, central tegmental tract—orange; ON, oculomotor nerve—purple; SCP, superior cerebellar peduncle—red; MLF, medial longitudinal fasciculus—blue; ML, medial lemniscus—green; LL, lateral lemniscus—yellow; PPTg, pedunculopontine tegmental nucleus—gray. (B) Sagittal view of the geometry of the modeled fiber pathways. (C) The FEM geometry, showing the lead location and grounded chamber. (D) Electric potential isosurfaces for the anisotropic and isotropic model.

Figure 2

Comparison of conductivity and diffusion tensors between Monkey L (top) and Monkey P (bottom). (A) The calculated conductivity, σ_xx, is shown for select coronal slices. (B) The distribution of conductivity values calculated from the primary, secondary, and tertiary eigenvalues for the entire brain (top) and the segmented brainstem (bottom). (C) The fractional anisotropy for a select brainstem slice (left), compared to a corresponding T1 slice (right). The diffusion tensors are plotted as spherical functions and overlaid on the fractional anisotropy. The orientations (dorsal-caudal, anterior-posterior, medial-lateral) are represented as RGB color components (i.e., R, G, and B, respectively).

Figure 3

Model-predicted activation of the ON fiber tract. Percent activation is plotted for each stimulation amplitude. Each column shows the variability of model predictions when changing axon diameter, conductivity scaling factor (s), and lead location. (Right) The axons activated at the motor threshold current for each contact are plotted.

Figure 4

Model-predicted activation of the SCP fiber tract. Percent activation is plotted for each stimulation amplitude. Each column shows the variability of model predictions when changing axon diameter, conductivity scaling factor (s), and lead location. (Right) The 0.5 mm lead displacement is shown in the context of the SCP axons. The axons activated at the PET stimulation amplitude for contact 4 (configuration 2) is shown.

Figure 5

Model-predicted activation of the CTG fiber tract. Percent activation is plotted for each stimulation amplitude. Each column shows the variability of model predictions when changing axon diameter, conductivity scaling factor (s), and lead location. (Right) The 0.5 mm lead displacement is shown in the context of the CTG axons. The axons activated at the PET stimulation amplitude for contact 7 (configuration 1) is shown.

Figure 6

PET imaging during PPTg-DBS. (Top) Co-registration of SWI and baseline PET/CT images. The SWI is shown in blue-green cold scale for differentiation from the gray CT. (Left) FDG-SUV during PET configuration 1 (0.9 mA stimulation through contact 7), normalized to OFF-DBS. The PET results are overlaid on SWI of Monkey L. (Right) FDG-SUV during PET configuration 2 (1.2 mA stimulation through contact 4), normalized to OFF-DBS.