A LASSO FOR HIERARCHICAL INTERACTIONS
- PMID: 26257447
- PMCID: PMC4527358
- DOI: 10.1214/13-AOS1096
A LASSO FOR HIERARCHICAL INTERACTIONS
Abstract
We add a set of convex constraints to the lasso to produce sparse interaction models that honor the hierarchy restriction that an interaction only be included in a model if one or both variables are marginally important. We give a precise characterization of the effect of this hierarchy constraint, prove that hierarchy holds with probability one and derive an unbiased estimate for the degrees of freedom of our estimator. A bound on this estimate reveals the amount of fitting "saved" by the hierarchy constraint. We distinguish between parameter sparsity-the number of nonzero coefficients-and practical sparsity-the number of raw variables one must measure to make a new prediction. Hierarchy focuses on the latter, which is more closely tied to important data collection concerns such as cost, time and effort. We develop an algorithm, available in the R package hierNet, and perform an empirical study of our method.
Keywords: Regularized regression; convexity; hierarchical sparsity; interactions; lasso.
Figures
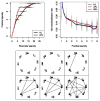



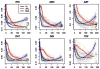
References
-
- Agresti A. Categorical Data Analysis. 2. Wiley-Interscience; New York: 2002.
-
- Bach F. Optimization with sparsity-inducing penalties. Foundations and Trends in Machine Learning. 2011;4:1–106.
-
- Bach F, Jenatton R, Mairal J, Obozinski G. Structured sparsity through convex optimization. Statist Sci. 2012;27:450–468.
-
- Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imaging Sci. 2009;2:183–202.
-
- Bickel P, Ritov Y, Tsybakov A. Inst Math Stat Collect. Vol. 6. Inst. Math. Statist; Beachwood, OH: 2010. Hierarchical selection of variables in sparse high-dimensional regression. Borrowing Strength: Theory Powering Applications—A Festschrift for Lawrence D. Brown; pp. 56–69.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
