Hierarchical Clustering With Prototypes via Minimax Linkage

Abstract

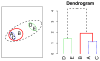
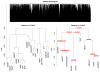
Agglomerative hierarchical clustering is a popular class of methods for understanding the structure of a dataset. The nature of the clustering depends on the choice of linkage-that is, on how one measures the distance between clusters. In this article we investigate minimax linkage, a recently introduced but little-studied linkage. Minimax linkage is unique in naturally associating a prototype chosen from the original dataset with every interior node of the dendrogram. These prototypes can be used to greatly enhance the interpretability of a hierarchical clustering. Furthermore, we prove that minimax linkage has a number of desirable theoretical properties; for example, minimax-linkage dendrograms cannot have inversions (unlike centroid linkage) and is robust against certain perturbations of a dataset. We provide an efficient implementation and illustrate minimax linkage's strengths as a data analysis and visualization tool on a study of words from encyclopedia articles and on a dataset of images of human faces.

Keywords: Agglomerative; Dendrogram; Unsupervised learning.

Figure 1

Agglomerative hierarchical clustering produces a sequence of clusterings that can be represented as a dendrogram. Each interior node of the dendrogram corresponds to a merging of two clusters (or points).

Figure 2

Complete, centroid, and minimax linkages. The solid black line represents the distance between the two clusters according to each linkage. The circle is of radius r(G ∪ H), where G and H denote the two clusters.

Figure 3

A “prototype-enhanced” minimax linkage dendrogram corresponding to the two-dimensional toy dataset shown in the right panel. Every interior node of the dendrogram has an associated prototype that we display. The height of each interior node is the maximum distance of any element in its branch to the prototype.

Figure 4

Successive cuts of a dendrogram with prototypes displayed: Cutting at height h yields a set of prototypes (shown in gray) such that every element of the dataset is covered by the set of balls of radius h centered at the prototypes. As h decreases, more prototypes are required.

Figure 5

Top: A branch of the minimax linkage tree for the Olivetti Faces dataset. The leaf images have been staggered vertically to prevent overlapping; the heights of the leaves do not have meaning. Prototype images are shown for the five highest nodes, summarizing the images below. Bottom: A subbranch of the above shows that the clustering has uncovered three angles of head position. This can be seen from the prototypes and is confirmed by looking at the leaves.

Figure 6

Top: The entire dendrogram of the Grolier’s Encyclopedia dataset offers little help as a visual tool because it is too dense and leaf labels do not fit. Lower: (Left) An “upper cut” view of the dendrogram above. A leaf with an asterisk indicates that it is the prototype representing a branch that has been cut away. (Note that what appear to be three-way splits are actually two consecutive splits that happen to be at the same height.) (Right) An exploded view of the music^* node on Left. This node represents a branch of 155 words; the upper cut of this branch is shown. The prototypes of each interior node are shown in italic type.

Figure 7

The maximum minimax radius is the farthest that any point lies from its cluster’s prototype. We see that minimax linkage hierarchical clustering does indeed do a better job of making this quantity small compared with the standard linkages. (Left) Olivetti Faces dataset. (Right) Grolier Encyclopedia dataset. The online version of this figure is in color.

Figure 8

Comparison of the smallest correlation of a sample to its cluster’s prototype (using minimax linkage hierarchical clustering) to the smallest correlation of a sample to its cluster’s centroid (using complete linkage hierarchical clustering). The online version of this figure is in color.

Figure 9

One-dimensional counterexample showing that minimax linkage cannot be written in terms of the Lance–Williams update formula.

Figure 10

Time comparison of the Rfunction hclust(complete linkage) with our implementation of minimax linkage. We find that hclust scales like n³, whereas our implementation of minimax linkage scales like n^2.4. The online version of this figure is in color.