GDSCalc: A Web-Based Application for Evaluating Discrete Graph Dynamical Systems
- PMID: 26263006
- PMCID: PMC4532456
- DOI: 10.1371/journal.pone.0133660
GDSCalc: A Web-Based Application for Evaluating Discrete Graph Dynamical Systems
Abstract
Discrete dynamical systems are used to model various realistic systems in network science, from social unrest in human populations to regulation in biological networks. A common approach is to model the agents of a system as vertices of a graph, and the pairwise interactions between agents as edges. Agents are in one of a finite set of states at each discrete time step and are assigned functions that describe how their states change based on neighborhood relations. Full characterization of state transitions of one system can give insights into fundamental behaviors of other dynamical systems. In this paper, we describe a discrete graph dynamical systems (GDSs) application called GDSCalc for computing and characterizing system dynamics. It is an open access system that is used through a web interface. We provide an overview of GDS theory. This theory is the basis of the web application; i.e., an understanding of GDS provides an understanding of the software features, while abstracting away implementation details. We present a set of illustrative examples to demonstrate its use in education and research. Finally, we compare GDSCalc with other discrete dynamical system software tools. Our perspective is that no single software tool will perform all computations that may be required by all users; tools typically have particular features that are more suitable for some tasks. We situate GDSCalc within this space of software tools.
Conflict of interest statement
Figures
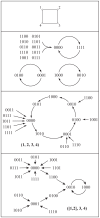


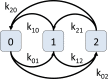
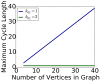


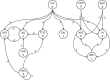
References
-
- Hatfield E, Cacioppo JT, Rapson RL (1994) Emotional Contagion. Cambridge University Press.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

