On the restricted mean survival time curve in survival analysis

Abstract

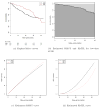
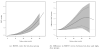
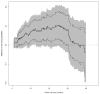
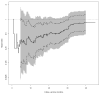
For a study with an event time as the endpoint, its survival function contains all the information regarding the temporal, stochastic profile of this outcome variable. The survival probability at a specific time point, say t, however, does not transparently capture the temporal profile of this endpoint up to t. An alternative is to use the restricted mean survival time (RMST) at time t to summarize the profile. The RMST is the mean survival time of all subjects in the study population followed up to t, and is simply the area under the survival curve up to t. The advantages of using such a quantification over the survival rate have been discussed in the setting of a fixed-time analysis. In this article, we generalize this approach by considering a curve based on the RMST over time as an alternative summary to the survival function. Inference, for instance, based on simultaneous confidence bands for a single RMST curve and also the difference between two RMST curves are proposed. The latter is informative for evaluating two groups under an equivalence or noninferiority setting, and quantifies the difference of two groups in a time scale. The proposal is illustrated with the data from two clinical trials, one from oncology and the other from cardiology.

Keywords: Equivalence/noninferiority study; Gaussian process; Martingale; Simultaneous confidence band; Survival function.

Figure 1

Results based on the data from ECOG (E4A03): (a) Kaplan-Meier curves for high-dose (solid line) and low-dose (dashed line) groups; (b) The estimated RMST (darker shaded region below the solid line) and RMTL (lighter shaded region above the solid line) up to 40 months for the low-dose group; (c) The estimated RMST curve for high-dose (solid line) and low-dose (dashed line) groups; (d) The estimated RMTL curve for high-dose (solid line) and low-dose (dashed line) groups.

Figure 2

Results based on the data from ECOG (E4A03): (a) RMTL curve for lowdose group; (b) Difference in RMST curves between low-dose and high-dose groups. Solid lines: point estimates, dashed lines: pointwise 0.95 confidence intervals, shaded region: simultaneous 0.95 confidence intervals, dotted line: zero reference line.

Figure 3

The difference in survival probability at different time points between lowdose and high-dose groups of patients in the ECOG (E4A03) study (Solid: point estimate; Dashed: 0.95 pointwise confidence interval; Shaded: 0.95 simultaneous confidence interval; dotted: zero reference line).

Figure 4

The hazard ratio for different censoring cutoff time points between low-dose and high-dose groups of patients in the ECOG (E4A03) study (Solid: point estimate; Dashed: 0.95 pointwise confidence interval; Shaded: 0.95 simultaneous confidence interval; dotted: one reference line).

Figure 5

The Kaplan-Meier estimates for the survival functions of patients taking ARB or ACEi in the VALIANT study.

Figure 6

The difference in RMST curves between ARB and ACEi in RMST up to time t of patients in the VALIANT study (Solid: point estimate; Dashed: 0.95 pointwise confidence interval; Shaded: 0.95 simultaneous confidence interval; dotted: zero reference line).