A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity
- PMID: 26308893
- PMCID: PMC4782800
- DOI: 10.1038/nature14971
A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity
Abstract
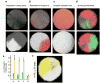
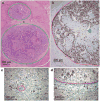
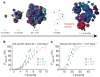
Most cancers in humans are large, measuring centimetres in diameter, and composed of many billions of cells. An equivalent mass of normal cells would be highly heterogeneous as a result of the mutations that occur during each cell division. What is remarkable about cancers is that virtually every neoplastic cell within a large tumour often contains the same core set of genetic alterations, with heterogeneity confined to mutations that emerge late during tumour growth. How such alterations expand within the spatially constrained three-dimensional architecture of a tumour, and come to dominate a large, pre-existing lesion, has been unclear. Here we describe a model for tumour evolution that shows how short-range dispersal and cell turnover can account for rapid cell mixing inside the tumour. We show that even a small selective advantage of a single cell within a large tumour allows the descendants of that cell to replace the precursor mass in a clinically relevant time frame. We also demonstrate that the same mechanisms can be responsible for the rapid onset of resistance to chemotherapy. Our model not only provides insights into spatial and temporal aspects of tumour growth, but also suggests that targeting short-range cellular migratory activity could have marked effects on tumour growth rates.
Figures








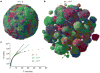

Comment in
-
Cancer: A moving target.Nature. 2015 Sep 10;525(7568):198-9. doi: 10.1038/nature15210. Epub 2015 Aug 26. Nature. 2015. PMID: 26308890 No abstract available.

