Estimation of noise properties for TV-regularized image reconstruction in computed tomography
- PMID: 26308968
- PMCID: PMC4850923
- DOI: 10.1088/0031-9155/60/18/7007
Estimation of noise properties for TV-regularized image reconstruction in computed tomography
Abstract
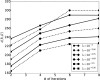
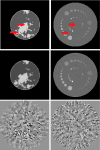
A method for predicting the image covariance resulting from total-variation-penalized iterative image reconstruction (TV-penalized IIR) is presented and demonstrated in a variety of contexts. The method is validated against the sample covariance from statistical noise realizations for a small image using a variety of comparison metrics. Potential applications for the covariance approximation include investigation of image properties such as object- and signal-dependence of noise, and noise stationarity. These applications are demonstrated, along with the construction of image pixel variance maps for two-dimensional 128 × 128 pixel images. Methods for extending the proposed covariance approximation to larger images and improving computational efficiency are discussed. Future work will apply the developed methodology to the construction of task-based image quality metrics such as the Hotelling observer detectability for TV-based IIR.
Figures




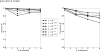
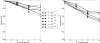






Similar articles
-
Iterative image-domain decomposition for dual-energy CT.Med Phys. 2014 Apr;41(4):041901. doi: 10.1118/1.4866386. Med Phys. 2014. PMID: 24694132
-
Simultaneous deblurring and iterative reconstruction of CBCT for image guided brain radiosurgery.Phys Med Biol. 2017 Apr 7;62(7):2521-2541. doi: 10.1088/1361-6560/aa5ed2. Epub 2017 Mar 1. Phys Med Biol. 2017. PMID: 28248652
-
Combined iterative reconstruction and image-domain decomposition for dual energy CT using total-variation regularization.Med Phys. 2014 May;41(5):051909. doi: 10.1118/1.4870375. Med Phys. 2014. PMID: 24784388
-
[Iterative reconstruction method in clinical CT examinations].Nihon Hoshasen Gijutsu Gakkai Zasshi. 2012;68(6):767-74. doi: 10.6009/jjrt.2012_jsrt_68.6.767. Nihon Hoshasen Gijutsu Gakkai Zasshi. 2012. PMID: 22805454 Review. Japanese. No abstract available.
-
Quantitative statistical methods for image quality assessment.Theranostics. 2013 Oct 4;3(10):741-56. doi: 10.7150/thno.6815. Theranostics. 2013. PMID: 24312148 Free PMC article. Review.
Cited by
-
Investigating simulation-based metrics for characterizing linear iterative reconstruction in digital breast tomosynthesis.Med Phys. 2017 Sep;44(9):e279-e296. doi: 10.1002/mp.12445. Med Phys. 2017. PMID: 28901614 Free PMC article.
References
-
- Sidky EY, Kao C-M, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. Journal of X-ray Science and Technology. 2006;14(2):119–139.
-
- Defrise M, Vanhove C, Liu X. An algorithm for total variation regularization in high-dimensional linear problems. Inverse Problems. 2011;27(6):065002.
-
- Jensen TL, Jrgensen JH, Hansen PC, Jensen SH. Implementation of an optimal first-order method for strongly convex total variation regularization. BIT Numerical Mathematics. 2012;52(2):329–356.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
