A positive feedback at the cellular level promotes robustness and modulation at the circuit level
- PMID: 26311181
- PMCID: PMC4620135
- DOI: 10.1152/jn.00471.2015
A positive feedback at the cellular level promotes robustness and modulation at the circuit level
Abstract
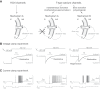
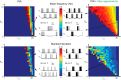
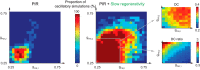
This article highlights the role of a positive feedback gating mechanism at the cellular level in the robustness and modulation properties of rhythmic activities at the circuit level. The results are presented in the context of half-center oscillators, which are simple rhythmic circuits composed of two reciprocally connected inhibitory neuronal populations. Specifically, we focus on rhythms that rely on a particular excitability property, the postinhibitory rebound, an intrinsic cellular property that elicits transient membrane depolarization when released from hyperpolarization. Two distinct ionic currents can evoke this transient depolarization: a hyperpolarization-activated cation current and a low-threshold T-type calcium current. The presence of a slow activation is specific to the T-type calcium current and provides a slow positive feedback at the cellular level that is absent in the cation current. We show that this slow positive feedback is required to endow the network rhythm with physiological modulation and robustness properties. This study thereby identifies an essential cellular property to be retained at the network level in modeling network robustness and modulation.
Keywords: central pattern generators; modulation; networks; postinhibitory rebound; robustness.
Copyright © 2015 the American Physiological Society.
Figures




References
-
- Angstadt JD, Grassmann JL, Theriault KM, Levasseur SM. Mechanisms of postinhibitory rebound and its modulation by serotonin in excitatory swim motor neurons of the medicinal leech. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 191: 715–732, 2005. - PubMed
-
- Brown TG. The intrinsic factors in the act of progression in the mammal. Proc R Soc Lond B 84: 308–319, 1911.
-
- Butera RJ Jr, Rinzel J, Smith JC. Models of respiratory rhythm generation in the prebötzinger complex. II. Populations of coupled pacemaker neurons. J Neurophysiol 82: 398–415, 1999. - PubMed
-
- Calabrese RL, De Schutter E. Motor-pattern-generating networks in invertebrates: modeling our way toward understanding. Trends Neurosci 15: 439–445, 1992. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

