Methanethiol Binding Strengths and Deprotonation Energies in Zn(II)-Imidazole Complexes from M05-2X and MP2 Theories: Coordination Number and Geometry Influences Relevant to Zinc Enzymes
- PMID: 26317178
- PMCID: PMC4942246
- DOI: 10.1021/acs.jpcb.5b07115
Methanethiol Binding Strengths and Deprotonation Energies in Zn(II)-Imidazole Complexes from M05-2X and MP2 Theories: Coordination Number and Geometry Influences Relevant to Zinc Enzymes
Abstract
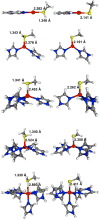
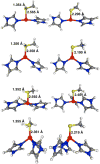
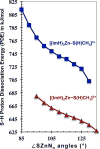
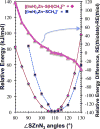
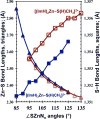
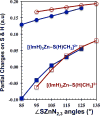
Zn(II) is used in nature as a biocatalyst in hundreds of enzymes, and the structure and dynamics of its catalytic activity are subjects of considerable interest. Many of the Zn(II)-based enzymes are classified as hydrolytic enzymes, in which the Lewis acidic Zn(II) center facilitates proton transfer(s) to a Lewis base, from proton donors such as water or thiol. This report presents the results of a quantum computational study quantifying the dynamic relationship between the zinc coordination number (CN), its coordination geometry, and the thermodynamic driving force behind these proton transfers originating from a charge-neutral methylthiol ligand. Specifically, density functional theory (DFT) and second-order perturbation theory (MP2) calculations have been performed on a series of [(imidazole)nZn-S(H)CH3](2+) and [(imidazole)nZn-SCH3](+) complexes with the CN varied from 1 to 6, n = 0-5. As the number of imidazole ligands coordinated to zinc increases, the S-H proton dissociation energy also increases, (i.e., -S(H)CH3 becomes less acidic), and the Zn-S bond energy decreases. Furthermore, at a constant CN, the S-H proton dissociation energy decreases as the S-Zn-(ImH)n angles increase about their equilibrium position. The zinc-coordinated thiol can become more or less acidic depending upon the position of the coordinated imidazole ligands. The bonding and thermodynamic relationships discussed may apply to larger systems that utilize the [(His)3Zn(II)-L] complex as the catalytic site, including carbonic anhydrase, carboxypeptidase, β-lactamase, the tumor necrosis factor-α-converting enzyme, and the matrix metalloproteinases.
Figures
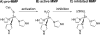
Similar articles
-
[(H2O)Zn(Imidazole)n]2+: the vital roles of coordination number and geometry in Zn-OH2 acidity and catalytic hydrolysis.Phys Chem Chem Phys. 2018 Oct 3;20(38):24979-24991. doi: 10.1039/c8cp03121e. Phys Chem Chem Phys. 2018. PMID: 30239541
-
Lewis acid properties of zinc(II) in Its cyclen complex. The structure of [Zn(cyclen)(S=C(NH2)2](ClO4)2 and the bonding of thiourea to metal ions. Some implications for zinc metalloenzymes.Inorg Chem. 2005 Apr 18;44(8):2791-7. doi: 10.1021/ic048705f. Inorg Chem. 2005. PMID: 15819567
-
Characterization of Zn(q+)-imidazole (q = 0, 1, 2) organometallic complexes: DFT methods vs. standard and explicitly correlated post-Hartree-Fock methods.Phys Chem Chem Phys. 2015 Jun 14;17(22):14417-26. doi: 10.1039/c4cp06108j. Phys Chem Chem Phys. 2015. PMID: 25920409
-
Efficient Calculation of Enzyme Reaction Free Energy Profiles Using a Hybrid Differential Relaxation Algorithm: Application to Mycobacterial Zinc Hydrolases.Adv Protein Chem Struct Biol. 2015;100:33-65. doi: 10.1016/bs.apcsb.2015.06.006. Epub 2015 Jul 15. Adv Protein Chem Struct Biol. 2015. PMID: 26415840 Review.
-
Marcus rate theory applied to enzymatic proton transfer.Biochim Biophys Acta. 2000 May 12;1458(1):88-103. doi: 10.1016/s0005-2728(00)00061-x. Biochim Biophys Acta. 2000. PMID: 10812026 Review.
Cited by
-
An S-methyltransferase that produces the climate-active gas dimethylsulfide is widespread across diverse marine bacteria.Nat Microbiol. 2024 Oct;9(10):2614-2625. doi: 10.1038/s41564-024-01788-6. Epub 2024 Aug 28. Nat Microbiol. 2024. PMID: 39198690 Free PMC article.
-
Synthesis, X-ray structure, in silico calculation, and carbonic anhydrase inhibitory properties of benzylimidazole metal complexes.J Enzyme Inhib Med Chem. 2018 Dec;33(1):1150-1159. doi: 10.1080/14756366.2018.1481404. J Enzyme Inhib Med Chem. 2018. PMID: 30001665 Free PMC article.
References
-
- Coleman JE. Zinc Proteins: Enzymes, Storage Proteins, Transcription Factors, and Replication Proteins. Annu Rev Biochem. 1992;61:897–946. - PubMed
-
- Andreini C, Banci L, Bertini I, Rosato A. Counting the Zinc-Proteins Encoded in the Human Genome. J Proteome Res. 2006;5:196–201. - PubMed
-
- Sousa SF, Lopes AB, Fernandes PA, Ramos MJ. The Zinc Proteome: A Tale of Stability and Functionality. Dalton Trans. 2009:7946–7956. - PubMed
-
- Auld DS. The Ins and Outs of Biological Zinc Sites. Biometals. 2009;22:141–148. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

