Longitudinal Mixed Membership Trajectory Models for Disability Survey Data

Abstract

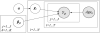
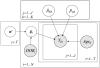
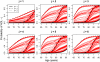
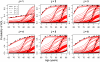
We develop new methods for analyzing discrete multivariate longitudinal data and apply them to functional disability data on U.S. elderly population from the National Long Term Care Survey (NLTCS), 1982-2004. Our models build on a mixed membership framework, in which individuals are allowed multiple membership on a set of extreme profiles characterized by time-dependent trajectories of progression into disability. We also develop an extension that allows us to incorporate birth-cohort effects, in order to assess inter-generational changes. Applying these methods we find that most individuals follow trajectories that imply a late onset of disability, and that younger cohorts tend to develop disabilities at a later stage in life compared to their elders.

Keywords: Cohort analysis; MCMC; Mixed Membership; Multivariate analysis; NLTCS; Trajectories.

Figure 1

Graphical probabilistic representation of the basic TGoM model. Observed variable Age_it is the age of individual i at survey wave t. Gray nodes represent observed quantities; white nodes represent parameters to estimate.

Figure 2

Probabilistic graphical representation of the extended TGoM model with cohort effects. Gray nodes represent observed quantities; white nodes represent parameters to estimate.

Figure 3

Posterior estimates of extreme profiles for models with K = 2, 3, 4. Vertical segments represent the age range at which ideal individuals’ probabilities of disability go up from 0.1 to 0.9, for each ADL ([Age_0.1,jk, Age_0.9,jk]]). For visualization purposes ADLs are sorted according to Age_0.5,jk posterior estimates.

Figure 4

Individual-level mixture of trajectories for model with K = 3 extreme profiles for each ADL. Extreme trajectories are represented with thick lines and and a random sample of 100 individual posterior trajectory curves are plotted using thin lines

Figure 5

Individual-level mixture of trajectories for model with K = 4 extreme profiles for each ADL. Extreme trajectories are represented with thick lines and and a random sample of 100 individual posterior trajectory curves are plotted using thin lines

Figure 6

Evolution of the parameter vector ξ across different generations for model with K = 2, 3 and 4 extreme profiles. The error bars show 95% equal tail posterior credible intervals associated with the kth component of the vector ξ.