Bayesian hierarchical grouping: Perceptual grouping as mixture estimation
- PMID: 26322548
- PMCID: PMC4593740
- DOI: 10.1037/a0039540
Bayesian hierarchical grouping: Perceptual grouping as mixture estimation
Abstract
We propose a novel framework for perceptual grouping based on the idea of mixture models, called Bayesian hierarchical grouping (BHG). In BHG, we assume that the configuration of image elements is generated by a mixture of distinct objects, each of which generates image elements according to some generative assumptions. Grouping, in this framework, means estimating the number and the parameters of the mixture components that generated the image, including estimating which image elements are "owned" by which objects. We present a tractable implementation of the framework, based on the hierarchical clustering approach of Heller and Ghahramani (2005). We illustrate it with examples drawn from a number of classical perceptual grouping problems, including dot clustering, contour integration, and part decomposition. Our approach yields an intuitive hierarchical representation of image elements, giving an explicit decomposition of the image into mixture components, along with estimates of the probability of various candidate decompositions. We show that BHG accounts well for a diverse range of empirical data drawn from the literature. Because BHG provides a principled quantification of the plausibility of grouping interpretations over a wide range of grouping problems, we argue that it provides an appealing unifying account of the elusive Gestalt notion of Prägnanz.
(c) 2015 APA, all rights reserved).
Figures


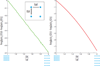



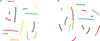
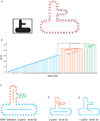
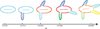






Similar articles
-
Bayesian contour integration.Percept Psychophys. 2001 Oct;63(7):1171-82. doi: 10.3758/bf03194532. Percept Psychophys. 2001. PMID: 11766942
-
An overview of quantitative approaches in Gestalt perception.Vision Res. 2016 Sep;126:3-8. doi: 10.1016/j.visres.2016.06.004. Epub 2016 Jul 4. Vision Res. 2016. PMID: 27353224 Review.
-
A tutorial for estimating Bayesian hierarchical mixture models for visual working memory tasks: Introducing the Bayesian Measurement Modeling (bmm) package for R.Behav Res Methods. 2025 Apr 14;57(5):144. doi: 10.3758/s13428-025-02643-0. Behav Res Methods. 2025. PMID: 40229483 Free PMC article.
-
Classical and Bayesian inference in neuroimaging: applications.Neuroimage. 2002 Jun;16(2):484-512. doi: 10.1006/nimg.2002.1091. Neuroimage. 2002. PMID: 12030833
-
Cortical algorithms for perceptual grouping.Annu Rev Neurosci. 2006;29:203-27. doi: 10.1146/annurev.neuro.29.051605.112939. Annu Rev Neurosci. 2006. PMID: 16776584 Review.
Cited by
-
Statistically defined visual chunks engage object-based attention.Nat Commun. 2021 Jan 11;12(1):272. doi: 10.1038/s41467-020-20589-z. Nat Commun. 2021. PMID: 33431837 Free PMC article.
-
Perceptual clustering in auditory streaming.PLoS Comput Biol. 2025 Jul 11;21(7):e1013189. doi: 10.1371/journal.pcbi.1013189. eCollection 2025 Jul. PLoS Comput Biol. 2025. PMID: 40644527 Free PMC article.
-
A computational model for gestalt proximity principle on dot patterns and beyond.J Vis. 2021 May 3;21(5):23. doi: 10.1167/jov.21.5.23. J Vis. 2021. PMID: 34015081 Free PMC article.
-
Simple Assumptions to Improve Markov Illuminance and Reflectance.Front Psychol. 2022 Jul 8;13:915672. doi: 10.3389/fpsyg.2022.915672. eCollection 2022. Front Psychol. 2022. PMID: 35874357 Free PMC article.
-
Hierarchical Constraints on the Distribution of Attention in Dynamic Displays.Behav Sci (Basel). 2024 May 11;14(5):401. doi: 10.3390/bs14050401. Behav Sci (Basel). 2024. PMID: 38785892 Free PMC article.
References
-
- Amir A, Lindenbaum M. A generic grouping algorithm and its quantitative analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1998;20(2):168–185.
-
- Anderson JR. The adaptive nature of human categorization. Psychological Review. 1991;98(3):409–429.
-
- Attias H. A variational Bayesian framework for graphical models. Advances in neural information processing systems. 2000;12(1–2):209–215.
-
- Attneave F. Some informational aspects of visual perception. Psychological Review. 1954;61:183–193. - PubMed
-
- August J, Siddiqi K, Zucker SW. Contour fragment grouping and shared, simple occluders. Computer Vision and Image Understanding. 1999;76(2):146–162.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

