Electro-osmotic flow in a rotating rectangular microchannel

Abstract

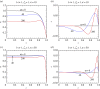
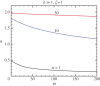
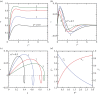
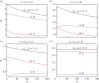
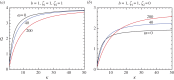
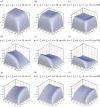
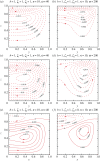
An analytical model is presented for low-Rossby-number electro-osmotic flow in a rectangular channel rotating about an axis perpendicular to its own. The flow is driven under the combined action of Coriolis, pressure, viscous and electric forces. Analytical solutions in the form of eigenfunction expansions are developed for the problem, which is controlled by the rotation parameter (or the inverse Ekman number), the Debye parameter, the aspect ratio of the channel and the distribution of zeta potentials on the channel walls. Under the conditions of fast rotation and a thin electric double layer (EDL), an Ekman-EDL develops on the horizontal walls. This is essentially an Ekman layer subjected to electrokinetic effects. The flow structure of this boundary layer as a function of the Ekman layer thickness normalized by the Debye length is investigated in detail in this study. It is also shown that the channel rotation may have qualitatively different effects on the flow rate, depending on the channel width and the zeta potential distributions. Axial and secondary flows are examined in detail to reveal how the development of a geostrophic core may lead to a rise or fall of the mean flow.

Keywords: Ekman layer; electric double layer; electro-osmotic flow; rotating channel; secondary flow.

Figure 1.

>Definition sketch of the problem: electro-osmotic flow through a rotating rectangular channel of height 2h and width 2b, with a zeta potential ζ₁ on the horizontal walls, and ζ₂ on the vertical walls. (Online version in colour.)

Figure 2.

Axial and transverse velocity profiles u(z),v(z) in a very wide channel b≫1, where (a) u(z) for κ=10, (b) v(z) for κ=10, (c) u(z) for κ=50, (d) v(z) for κ=50. (Online version in colour.)

Figure 3.

Flow rate per unit width q in a very wide channel b≫1 as a function of the rotation parameter ω. (Online version in colour.)

Figure 4.

For flow in an Ekman–EDL: (a) axial velocity profiles u(z*), (b) transverse velocity profiles v(z*), (c) Ekman spirals, (d) $z_m^{\ast }$ and $u_{\mathrm{\infty }}$ as functions of κ*, where $z_m^{\ast }$ is the height at which u is the maximum, and $u_{\mathrm{\infty }}$ is the limit of u as $z^{\ast }\to \mathrm{\infty }$. (Online version in colour.)

Figure 5.

Flow rate Q in a channel of finite width as a function of the rotation parameter ω, where κ=10, and (a) b=2, (b) b=1, (c) b=0.5 and (d) b=0.2. Three cases are considered: all walls are charged (AWC) when (ζ₁,ζ₂)=(1,1), only vertical walls are charged (VWC) when (ζ₁,ζ₂)=(0,1) and only horizontal walls are charged (HWC) when (ζ₁,ζ₂)=(1,0). (Online version in colour.)

Figure 6.

Flow rate Q in a square channel b=1 as a function of the Debye parameter κ, for (a) AWC, (b) HWC. (Online version in colour.)

Figure 7.

Axial velocity profiles u(y,z) in a square channel b=1, where κ=10, and for AWC: (a) ω=0, (b) ω=40, (c) ω=200; for VWC: (d) ω=0, (e) ω=40, (f) ω=200; for HWC: (g) ω=0, (h) ω=40, (i) ω=200. (Online version in colour.)

Figure 8.

Streamlines show the secondary flow fields in a square channel b=1, where κ=10, and for AWC: (a) ω=40, (b) ω=200; for VWC: (c) ω=40, (d) ω=200; for HWC: (e) ω=40, (f) ω=200. (Online version in colour.)