Mitigation of impedance changes due to electroporation therapy using bursts of high-frequency bipolar pulses

Abstract

Background: For electroporation-based therapies, accurate modeling of the electric field distribution within the target tissue is important for predicting the treatment volume. In response to conventional, unipolar pulses, the electrical impedance of a tissue varies as a function of the local electric field, leading to a redistribution of the field. These dynamic impedance changes, which depend on the tissue type and the applied electric field, need to be quantified a priori, making mathematical modeling complicated. Here, it is shown that the impedance changes during high-frequency, bipolar electroporation therapy are reduced, and the electric field distribution can be approximated using the analytical solution to Laplace's equation that is valid for a homogeneous medium of constant conductivity.

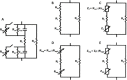
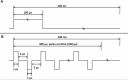
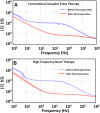
Methods: Two methods were used to examine the agreement between the analytical solution to Laplace's equation and the electric fields generated by 100 µs unipolar pulses and bursts of 1 µs bipolar pulses. First, pulses were applied to potato tuber tissue while an infrared camera was used to monitor the temperature distribution in real-time as a corollary to the electric field distribution. The analytical solution was overlaid on the thermal images for a qualitative assessment of the electric fields. Second, potato ablations were performed and the lesion size was measured along the x- and y-axes. These values were compared to the analytical solution to quantify its ability to predict treatment outcomes. To analyze the dynamic impedance changes due to electroporation at different frequencies, electrical impedance measurements (1 Hz to 1 MHz) were made before and after the treatment of potato tissue.

Results: For high-frequency bipolar burst treatment, the thermal images closely mirrored the constant electric field contours. The potato tissue lesions differed from the analytical solution by 39.7 ± 1.3 % (x-axis) and 6.87 ± 6.26 % (y-axis) for conventional unipolar pulses, and 15.46 ± 1.37 % (x-axis) and 3.63 ± 5.9 % (y-axis) for high- frequency bipolar pulses.

Conclusions: The electric field distributions due to high-frequency, bipolar electroporation pulses can be closely approximated with the homogeneous analytical solution. This paves way for modeling fields without prior characterization of non-linear tissue properties, and thereby simplifying electroporation procedures.

Figure 1

Functional circuit models representing a single cell exposed to different pulsing waveforms at various stages of electroporation. A common electrical model was used to represent an intact cell (A). Prior to the onset of electroporation, the membrane capacitance can be considered as an open circuit during conventional unipolar pulse treatment (B), while the contribution of the reactive component to the effective membrane impedance persists for high-frequency bipolar bursts (C). Once membrane permeabilization begins, the equivalent membrane impedance reduces due to electroporation for both the conventional unipolar pulses (D) and high-frequency bipolar bursts (D).

Figure 2

Pulse waveforms delivered to the potato tissue during pulsing in their idealized form. For unipolar pulse treatment, pulse widths of 100 µs were delivered at a pulse repetition frequency of 10 Hz (100 ms duty cycle) for 80 pulses (A). For high-frequency bipolar bursts, 50 bipolar pulses (1 µs positive, 2 µs delay, 1 µs negative, 2 µs delay) were delivered at a burst repetition frequency of 10 Hz (100 ms duty cycle) for 80 bursts.

Figure 3

Representative thermal images overlaid with the corresponding electrical field contours from the analytical solution of the Laplace's equation, using the electrode insertions as the reference points for the mapping. Thermal image of high-frequency bipolar treatment was overlaid with the electric field analytical solution at 3000 V/cm, 600 V/cm, 350 V/cm, 240 V/cm, and 160 V/cm going outward from electrode (A). Thermal image of conventional unipolar treatment was overlaid with the electric field analytical solution at 3000 V/cm, 500 V/cm, 300 V/cm, 200 V/cm, and 120 V/cm going outward from electrode (B).

Figure 4

Laplace's equation more accurately represents the lesion geometry generated by high-frequency bipolar bursts. Lesions obtained due to conventional unipolar treatment with 80 pulses of 400 V, 100 µs duration, and pulse repetition rate of 1 Hz were overlaid with Laplace's solution contour plotted for 80 V/cm electric field intensity (A). Lesions obtained due to high-frequency bipolar burst treatment with 80 bursts of 1020 V, 100 µs on time, and pulse repetition rate of 1 Hz were overlaid with Laplace's solution contour plotted for 350 V/cm electric field intensity (B). Thresholded lesion geometry from image A (C) and image B (D).

Figure 5

Frequency spectrum (95% confidence interval around mean) obtained prior to and after treatment of potato tissue with conventional unipolar pulses and high-frequency bipolar bursts showing similar shifts in impedance spectra. Blue dotted line indicates the frequency spectrum obtained prior to treatment with unipolar pulses. Solid red line indicates frequency spectrum obtain after treatment of tissue with unipolar pulses (A). Blue dotted line indicates the frequency spectrum obtained prior to treatment with high-frequency bipolar bursts. Solid red line indicates frequency spectrum obtain after treatment of tissue with high-frequency bipolar bursts (B).

Figure 6

A power spectral analysis of the input waveforms - conventional unipolar pulse (A) and a high-frequency bipolar burst (B) was obtained.