Some Health States Are Better Than Others: Using Health State Rank Order to Improve Probabilistic Analyses

Abstract

Background: Probabilistic sensitivity analyses (PSA) may lead policy makers to take nonoptimal actions due to misestimates of decision uncertainty caused by ignoring correlations. We developed a method to establish joint uncertainty distributions of quality-of-life (QoL) weights exploiting ordinal preferences over health states.

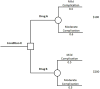
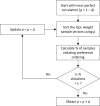
Methods: Our method takes as inputs independent, univariate marginal distributions for each QoL weight and a preference ordering. It establishes a correlation matrix between QoL weights intended to preserve the ordering. It samples QoL weight values from their distributions, ordering them with the correlation matrix. It calculates the proportion of samples violating the ordering, iteratively adjusting the correlation matrix until this proportion is below an arbitrarily small threshold. We compare our method with the uncorrelated method and other methods for preserving rank ordering in terms of violation proportions and fidelity to the specified marginal distributions along with PSA and expected value of partial perfect information (EVPPI) estimates, using 2 models: 1) a decision tree with 2 decision alternatives and 2) a chronic hepatitis C virus (HCV) Markov model with 3 alternatives.

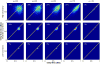
Results: All methods make tradeoffs between violating preference orderings and altering marginal distributions. For both models, our method simultaneously performed best, with largest performance advantages when distributions reflected wider uncertainty. For PSA, larger changes to the marginal distributions induced by existing methods resulted in differing conclusions about which strategy was most likely optimal. For EVPPI, both preference order violations and altered marginal distributions caused existing methods to misestimate the maximum value of seeking additional information, sometimes concluding that there was no value.

Conclusions: Analysts can characterize the joint uncertainty in QoL weights to improve PSA and value-of-information estimates using Open Source implementations of our method.

Keywords: bias; correlated parameters; expected value of partial perfect information; joint distribution; parameter correlation; probabilistic sensitivity analysis; value of information.

Figure B1

Markov States for Example Model 1.

Figure 1

Algorithm for the Simplified 2 Health State Version of the correlated distributions method. This algorithm shows the core concept in our approach which balances correlation between samples (?) with the percent of samples violating the preference order. The algorithm starts with near-perfect correlation and reduces this correlation by a pre-defined decrement (?) until the percent of samples violating the preference order reaches a tolerance threshold (?).

Figure 2

Violations of health state preference order for different levels of correlation in the joint uncertainty distributions for QoL weights of mild and moderate complications. The joint distribution of QoL weights for the utility of being in the mild health state (x-axis) and in the moderate health state (y-axis) are shown for 10,000 random samples. The plots show the relationship of the percent of samples violating the preference rank ordering of U(mild) > U(moderate) for 5 levels of correlations between these two QoL weights and 3 levels of uncertainty in the distributions of the QoL weights (the percentages in the upper left corner of each subplot show the proportion of samples resulting in violations). As expected, increasing correlations, reducing uncertainty, or both decreases the proportions of samples resulting in violations. Utility of Mild is distributed as beta(7,3), and utility of Moderate as beta(6.5, 3.5) at moderate level of uncertainty. Notice that the mean of the distribution stays constant (0.7 and 0.65 for Mild and Moderate, respectively) at all levels of correlation and uncertainty.

Figure 3

Performance comparison of our method (induced-correlations) to existing methods for capturing the joint uncertainty distribution of QoL weights. Panels A and B compare the performance of our approach (Induced-Correlations) to four other approaches involving avoiding preference rank order violations for Example Mode1 and Example Model 2, respectively. Performance involves simultaneous assessment on two different scales: (1) the percent of samples violating the preference rank order with each the method (x-axis), and (2) how much the CDFs of the QoL weight uncertainty distributions change with each method compared to the specified marginal distributions without correlation (y-axis). The optimal point (no rank violations and no difference in CDF) is marked with the arrow. Our approach does not change the marginal distribution (0 CDF violations) and induces approximately 5% sample violations as per the epsilon we set, which can be made arbitrarily small. Panel C shows the effect of increased uncertainty on these performance metrics for Example Model 1. As expected, the performance of all methods improves when uncertainty is low as shown by the proximity of all methods to the optimal point indicated by the arrow. Our approach continues to perform relatively well even at higher uncertainty levels where existing methods’ performance tends to degrade appreciably.