Strong interface-induced spin-orbit interaction in graphene on WS2
- PMID: 26391068
- PMCID: PMC4595714
- DOI: 10.1038/ncomms9339
Strong interface-induced spin-orbit interaction in graphene on WS2
Abstract
Interfacial interactions allow the electronic properties of graphene to be modified, as recently demonstrated by the appearance of satellite Dirac cones in graphene on hexagonal boron nitride substrates. Ongoing research strives to explore interfacial interactions with other materials to engineer targeted electronic properties. Here we show that with a tungsten disulfide (WS2) substrate, the strength of the spin-orbit interaction (SOI) in graphene is very strongly enhanced. The induced SOI leads to a pronounced low-temperature weak anti-localization effect and to a spin-relaxation time two to three orders of magnitude smaller than in graphene on conventional substrates. To interpret our findings we have performed first-principle electronic structure calculations, which confirm that carriers in graphene on WS2 experience a strong SOI and allow us to extract a spin-dependent low-energy effective Hamiltonian. Our analysis shows that the use of WS2 substrates opens a possible new route to access topological states of matter in graphene-based systems.
Figures


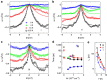

References
-
- Kane C. L. & Mele E. J. Z(2) topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005). - PubMed
-
- Kane C. L. & Mele E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005). - PubMed
-
- Huertas-Hernando D., Guinea F. & Brataas A. Spin-orbit coupling in curved graphene, fullerenes, nanotubes, and nanotube caps. Phys. Rev. B 74, 155426 (2006).
-
- Min H. et al.. Intrinsic and Rashba spin-orbit interactions in graphene sheets. Phys. Rev. B 74, 165310 (2006).
-
- Konschuh S., Gmitra M. & Fabian J. Tight-binding theory of the spin-orbit coupling in graphene. Phys. Rev. B 82, 245412 (2010).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

