Fiber ball imaging
- PMID: 26432187
- PMCID: PMC4651772
- DOI: 10.1016/j.neuroimage.2015.09.049
Fiber ball imaging
Abstract
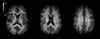
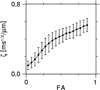
By modeling axons as thin cylinders, it is shown that the inverse Funk transform of the diffusion MRI (dMRI) signal intensity obtained on a spherical shell in q-space gives an estimate for a fiber orientation density function (fODF), where the accuracy improves with increasing b-value provided the signal-to-noise ratio is sufficient. The method is similar to q-ball imaging, except that the Funk transform of q-ball imaging is replaced by its inverse. We call this new approach fiber ball imaging. The fiber ball method is demonstrated for healthy human brain, and fODF estimates are compared to diffusion orientation distribution function (dODF) approximations obtained with q-ball imaging. The fODFs are seen to have sharper features than the dODFs, reflecting an enhancement of the higher degree angular frequencies. The inverse Funk transform of the dMRI signal intensity data provides a simple and direct method of estimating a fODF. In addition, fiber ball imaging leads to an estimate for the ratio of the fraction of MRI visible water confined to the intra-axonal space divided by the square root of the intra-axonal diffusivity. This technique may be useful for white matter fiber tractography, as well as other types of microstructural modeling of brain tissue.
Keywords: Brain; Diffusion MRI; Fiber orientation density function; Funk transform; High-angular-resolution diffusion imaging; Q-ball imaging.
Copyright © 2015 Elsevier Inc. All rights reserved.
Figures




References
-
- Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992 Dec 11;598(1–2):143–153. - PubMed
-
- Abramowitz M, Stegun IA. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. Dover, New York: 1972.
-
- Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magn. Reson. Med. 2005 Nov;54(5):1194–1206. - PubMed
-
- Assaf Y, Cohen Y. Assignment of the water slow-diffusing component in the central nervous system using q-space diffusion MRS: implications for fiber tract imaging. Magn Reson Med. 2000 Feb;43(2):191–199. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

