A quantitative framework for whole-body coordination reveals specific deficits in freely walking ataxic mice

Abstract

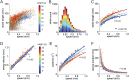
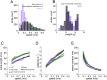
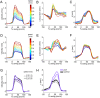
The coordination of movement across the body is a fundamental, yet poorly understood aspect of motor control. Mutant mice with cerebellar circuit defects exhibit characteristic impairments in locomotor coordination; however, the fundamental features of this gait ataxia have not been effectively isolated. Here we describe a novel system (LocoMouse) for analyzing limb, head, and tail kinematics of freely walking mice. Analysis of visibly ataxic Purkinje cell degeneration (pcd) mice reveals that while differences in the forward motion of individual paws are fully accounted for by changes in walking speed and body size, more complex 3D trajectories and, especially, inter-limb and whole-body coordination are specifically impaired. Moreover, the coordination deficits in pcd are consistent with a failure to predict and compensate for the consequences of movement across the body. These results isolate specific impairments in whole-body coordination in mice and provide a quantitative framework for understanding cerebellar contributions to coordinated locomotion.

Keywords: Purkinje cell; ataxia; cerebellum; locomotion; mouse; neuroscience.

Figure 1.. LocoMouse system for analyzing mouse locomotor coordination.

(A) LocoMouse apparatus. The mouse walks freely across a glass corridor with mirror below at a 45° angle. A single high-speed camera captures side and bottom views at 400 fps. Infrared (IR) sensors trigger data collection. (B) Machine learning algorithms identify paws, nose and tail segments and track their movements in 3D. Example ‘paw’ and ‘not paw’ training images for SVM (Support Vector Machine) feature detectors are shown for side and bottom views. (C) Continuous tracks are obtained by post-processing the feature detections with a Multi-Target Tracking algorithm. (D) Continuous forward trajectories (x position vs time) for paws, nose, and tail. The inset illustrates the color code used throughout the paper to identify individual features. (E) Continuous vertical (z) trajectories of the two front paws. (F) Side-to-side (y) position of proximal (green) to distal (yellow) tail segments vs time. (G) Individual strides were divided into swing and stance phases for further analysis. Further validation of tracking algorithm is presented in Figure 1—figure supplement 1. DOI: http://dx.doi.org/10.7554/eLife.07892.003

Figure 1—figure supplement 1.. LocoMouse tracking validation.

(A) Comparison of manual (gray) and automated tracking (blue) for front left paw across 3 dimensions. From left to right, plots show normalized x, y, and z paw position aligned to stance onset (n = 43 strides from 9 movies of 3 mice). (B) Scatterplots of manual vs automated tracking positions (x, y, and z) for all frames (n = 4194) of the same 9 movies. Values where the difference between manual and automated tracking are larger than average paw size are color-coded in green. Correlation coefficients are Pearson's r. (C) Example tracking traces demonstrate that stride lengths can differ at similar walking speeds due to pauses in walking. DOI: http://dx.doi.org/10.7554/eLife.07892.004

Figure 2.. Basic stride parameters can be predicted using only walking speed and body size.

(A) Stride length vs walking speed for 9602 individual strides of the front right paws of 34 wildtype mice are color-coded by weight for each individual animal. More information on the mice can be found in Figure 2—figure supplement 1 and Figure 2—source data 1. (B) Histogram of average walking speeds for each stride from (A). Strides are divided into speed bins of 0.05 m/s. (C–F) Stride length, cadence (1/stride duration), swing velocity, and stance duration vs walking speed, respectively. For each parameter, speed-binned median values are shown for each animal (solid circles, color coded by weight). Data for each animal are connected across speeds with a thin dotted line. Thick lines are the output of the linear mixed-effects model, for 3 example weights across walking speeds (blue: 9g, cyan:19g, red: 33g). Marginal R-squared values for each linear mixed model are shown for each parameter. All raw data for Figure 2 and Figure 2—figure supplement 1 can be found in Figure 2—source data 1. DOI: http://dx.doi.org/10.7554/eLife.07892.006

Figure 2—figure supplement 1.. Using linear mixed effects models to predict basic stride parameters.

(A) Properties of wildtype mice used for linear mixed-effects model. A total of 34 wild-type C57BL/6 mice were used for the linear mixed-effects model in Figure 2. Each individual WT animal is plotted as a circle (open circles, females, N = 11; closed circles, males, N = 23). Symbols are color-coded by age. The diverse group included a variety of ages (30–114 days), body lengths (61–100 mm), and weights (7–33g). (B) Comparison of model fits for basic stride parameters. Speed, gender, age, body length, weight (fixed terms) and subject (random term) were used as predictor variables in the linear mixed-effects model. Table rows show tested equations for predicting stride parameters and values used for selection criteria of the resulting predictive model. p-values reported for each term are the outcome of a likelihood ratio test comparing indicated equations (superscripts). The last two lines (f, g) indicate that age and gender did not improve the predictions beyond the inclusion of speed and body weight. (C) Coefficients of speed and weight for basic stride parameters. The final equations for each stride parameter included speed and weight as fixed-term predictor variables; subject was included as a random-term. Coefficient values for fixed terms are represented. These equations can be used to predict stride parameters for a given mouse walking at a particular speed. DOI: http://dx.doi.org/10.7554/eLife.07892.008

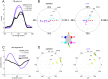
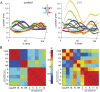
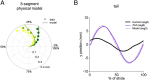
Figure 3.. Differences in forward paw trajectories in pcd can be accounted for by walking speed and body size; impairments are restricted to off-axis movement.

(A) Histogram of walking speeds, divided into 0.05 m/s speed bins for pcd (purple N = 3 mice; n = 3052 strides) and littermate controls (green, N = 7; n = 2256 strides). (B–D) Stride length (B), cadence (C, 1/stride duration) and stance duration (D) vs walking speed for pcd mice (purple) and littermate controls (green). For each parameter, the thin lines with shadows represent median values ±25th, 75th percentiles. Thick lines represent the predictions calculated using the mixed-effect models described in Figure 2 and Figure 2—figure supplement 1 (including speed and weight as predictor variables). (E) Average instantaneous forward (x) velocity of FR paw during swing phase for pcd (purple) and size-matched controls (black). Line thickness represents increasing speed. (F) x-y position of four paws relative to the body center during swing. (G) y-excursion for front and hind paws, relative to body midline. (H) Average vertical (z) position of FR paw relative to ground during swing. DOI: http://dx.doi.org/10.7554/eLife.07892.010

Figure 3—figure supplement 1.. Basic stride parameters for pcd are are not different from their size-matched controls.

(A) Histogram of walking speeds, divided in 0.05 m/s speed bins for pcd (purple, N = 3 mice, n = 3052 strides), littermate controls (green, N = 7 mice, n = 2256 strides) and size matched controls (black, N = 11 mice, n = 3400 strides). (B) Histogram of stride counts by weight for size-matched controls and pcd. (C–E) Basic stride parameters. For each parameter, thick lines represent the prediction, from the mixed-effects models derived from wildtype data in Figure 2 (including speed and weight as predictor variables), for each group. Pcd (average weight = 12g; purple line), control littermates (average weight = 26g; blue line) and size-match controls (average weight = 12g; black line). (C) Stride length values vs walking speed for pcd, littermate controls and size-matched controls (median ±25th, 75th percentile). Data are represented by thin lines and shadows, thick lines are model predictions. (D, E) Temporal measures of the step cycle; cadence (inverse of stride duration) and stance duration, respectively (median ±25th, 75th percentile). DOI: http://dx.doi.org/10.7554/eLife.07892.011

Figure 3—figure supplement 2.. 3D paw trajectories for wildtype controls and pcd.

(A–C) Average 3D trajectories for front right paw of wildtype control group (N = 34; n = 9602 strides) during swing phase. Traces are binned and color coded by walking speed. (A) Instantaneous forward (x) velocity. (B) side-to-side (y) excursion (C) vertical (z) position relative to ground. (D–F) Same as above but for hind right paw of wildtype control group. (G–I) Paw trajectories for pcd and size-matched controls. (G) Hind right paw x-trajectories. (H) Hind right paw vertical (z) position relative to ground during swing. In pcd, hind paws were lifted higher than forepaws, and their peak positions varied more steeply with speed, (F[153.02,1] = 5.64,p < 0.05). DOI: http://dx.doi.org/10.7554/eLife.07892.012

Figure 4.. Front-hind limb coordination is specifically impaired in pcd.

(A) Polar plots indicating the phase of the step cycle in which each limb enters stance, aligned to stance onset of FR paw (red). Distance from the origin represents walking speed. Left, size-matched control mice (N = 11). Right, pcd (N = 3). (B) Left-right phase (left) and front-hind (right) phase for individual animals of pcd and size-matched controls. Circles show average values for each animal. Lines show fit of linear-mixed effects model for each variable. (C) Average Hildebrand plots aligned to FR stance onset for speeds between 0.15 and 0.20 m/s. Grayscale represents probably of stance. (D) Area plot of average paw support types as % of stride cycle, across speeds for size-matched controls (left) and pcd (right). (E) 3 paw (left) and 2-paw other (right) supports for each animal (circles). Lines show fit of linear-mixed effects model. (F) Average ±sem percent double support for hind paws of pcd and size-matched controls. (G) Coefficient of variation for paw placement distance (front-hind) for pcd and size-matched controls. DOI: http://dx.doi.org/10.7554/eLife.07892.013

Figure 4—figure supplement 1.. Comparison of gait patterns between control and pcd mice.

(A) Smoothed probability density of diagonal (FL-HR) pair stance phase lags and speed obtained by kernel density estimation for all strides of size-matched controls (left, n = 3400, N = 11) and pcd (right, n = 3052, N = 3). Color code is estimated stride density. (B) Smoothed probability density of ipsilateral pair (FL-HL) stance phase lags and % stance duration for all strides of size-matched controls (left) and pcd (right), plotted according to the convention of Figure 5 of Hildebrand (1989). Color code is estimated stride density. (C) Polar plots of stance to swing phasing aligned to front right paw for controls (left) and pcd (right). DOI: http://dx.doi.org/10.7554/eLife.07892.014

Figure 5.. The tail and nose movements of pcd mice can be modeled as a passive consequence of the forward motion of the hind limbs.

(A, B) Averaged lateral trajectory of tail segment 8 (A) and nose (B), relative to the mid-point between the hind paws, for animals walking at 0.25–0.30 m/s, for size-matched controls (black), pcds (purple) and model (dashed gray). (C) Geometric model of the tail and nose. The lateral position of each tail segment at every time step is given by S_yi =_AS_isinθ, whereas the lateral position of the nose is given by N_y=_DN _sinλ. (D, E) Phase of maximum correlation between the forward position of the hind paws and the lateral trajectories of each tail segment (green-yellow gradient) and the nose (orange). (F) The maximum correlation phases of the passive geometric model (lines) are superimposed on the observed values (circles) for tail segments 1 (dark green), 8 (light green), 15 (yellow), and nose (orange). DOI: http://dx.doi.org/10.7554/eLife.07892.015

Figure 5—figure supplement 1.. Nose and tail movements across speed bins.

(A–C) Average interpolated (y) trajectory of segment 1, 8, 15, respectively for wild type mice aligned with stance onset of the hind right paw. (D) Average interpolated (y) trajectory of nose for wild type mice aligned with stance onset of the front right paw. (E–G). Average interpolated (y) trajectory of all tail segments for pcd mice aligned to stance onset of the hind right paw across several speed bins. (H) Bode plot of tail and nose phases for pcd. DOI: http://dx.doi.org/10.7554/eLife.07892.016

Figure 5—figure supplement 2.. Results summary for young pcd and size-matched controls.

(A) Average vertical (z) position of FR paw relative to ground during swing for young (<P55) pcd (purple) and size-matched controls (compare with Figure 3G). Line thickness represents increasing speed. (B–D) Polar plots indicating the phase of the step cycle in which each limb enters stance, aligned to stance onset of FR paw (red). Distance from the origin represents walking speed. Left, size-matched control mice. Right, young pcd (compare with Figure 4A). (C) Averaged lateral trajectory of tail segment 8 relative to the mid-point between the hind paws, for animals walking at 0.1–0.2 m/s, for size-matched controls (black), and young pcd (purple) (compare with Figure 5A). (D) Phase of maximum correlation between the forward position of the hind paws and the lateral trajectories of each tail segment (green-yellow gradient) for size-matched controls (left) and pcd (right) (compare with Figure 5D,E). DOI: http://dx.doi.org/10.7554/eLife.07892.017

Figure 6.. Visualization of impaired whole-body coordination in pcd.

(A) Ribbon plots showing average vertical (z) trajectories for nose, paw and select tail (2, 5, 8, 11, 14) segments for size-matched control (Left, N = 11)) and pcd (Right, N = 3) mice walking at 0.20–0.25 m/s. Data are presented relative to 100% of the stride cycle of the FR paw (x-axis). Nose and paw trajectories are z position relative to floor; tail is z relative to floor with mean vertical position of the of base of the tail subtracted for clarity. (B) Matrix of correlation coefficients computed for average vertical trajectories of control (Left) and pcd (Right). Color bar is value of correlation coefficient. DOI: http://dx.doi.org/10.7554/eLife.07892.019

Author response image 1.. Stance to swing phases for size-matched controls and all pcd.

DOI: http://dx.doi.org/10.7554/eLife.07892.023

Author response image 2.. Average Hildebrand plots aligned to FR stance onset.

DOI: http://dx.doi.org/10.7554/eLife.07892.024

Author response image 3.. Physical model.

The physical model of the tail consists of three masses 1, 2 and 3 (the later being the most distal) connected via an angualar spring-damper system. The masses of each segment were estimated from measurements of a real mouse tail (10g, 0.6g, 0.001g for segments 1, 2 and 3 respectively). The springs and dampers were estimated manually (k₁=13e-6 Nm/deg, c₁=0.95e-6 Nms/deg, k₂=5e-6 Nm/deg, c₂=0.7e-6 Nms/deg and k₃=20e-6 Nm/deg, c₃=0.2e-6 Nms/deg). The model was implemented and tested in SimMechanics MATLAB 2015a. (A) The phases of segments 1, 2 and 3 in the model (lines) superimposed over segments of 18 and 15 of the pcd tail. (B) Trajectories of tail segment 8 for controls (black), and pcd (purple), and tail segment 2 for the physical model. DOI: http://dx.doi.org/10.7554/eLife.07892.025