Reconstruction of ancestral gene orders using intermediate genomes

Abstract

Background: The problem of reconstructing ancestral genomes in a given phylogenetic tree arises in many different comparative genomics fields. Here, we focus on reconstructing the gene order of ancestral genomes, a problem that has been largely studied in the past 20 years, especially with the increasing availability of whole genome DNA sequences. There are two main approaches to this problem: event-based methods, that try to find the ancestral genomes that minimize the number of rearrangement events in the tree; and homology-based, that look for conserved structures, such as adjacent genes in the extant genomes, to build the ancestral genomes.

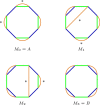
Results: We propose algorithms that use the concept of intermediate genomes, arising in optimal pairwise rearrangement scenarios. We show that intermediate genomes have combinatorial properties that make them easy to reconstruct, and develop fast algorithms with better reconstructed ancestral genomes than current event-based methods. The proposed framework is also designed to accept extra information, such as results from homology-based approaches, giving rise to combined algorithms with better results than the original methods.

Figure 1

Genome G = {(○ 1 −2 3 ○), (○ 4 5 ○)} with adjacency set A = {○1^t, 1^h 2^h, 2^t 3^t, 3^h ○, ○4^t, 4^h 5^t, 5^h○}.

Figure 2

Breakpoint graph BP(A, B) of A = {○1^t, 1^h 2^t, 2^h 3^t, 3^h 4^t, 4^h ○, ○5^t, 5^h6^t, 6^h 7^t, 7^h ○} and B = {1^h 2^h, 2^t 3^h, 3^t 4^t, 4^h 1^t, ○6^t, 6^h 5^t, 5^h 7^h, 7^t○}. A-edges are drawn in green, and B-edges in blue.

Figure 3

Circular BP graph BP(A, B) of the genomes in Figure 2, with telomeric adjacencies. A-edges are drawn in green, and B-edges in blue.

Figure 4

Possible ways of applying a DCJ operation on adjacencies pq and rs. (a) The initial BP(A, B); (b) Applying DCJ {pq, rs} → {ps, qr} on genome A; (c) Applying {pq, rs} → {pr, qs} on genome A; The DCJ in (b) is optimal, increasing the number of cycles by one. The DCJ in (c) is not, and introduces crossing edges.

Figure 5

Scenario $\mathcal{ S}$= {A = M₀ , M₁ , M₂ , M₃ = B} transforming A (green edges) into B (blue edges) with DCJ operations, shown in BP(A, B). Intermediate genomes M_i are drawn at each step with orange edges. At each step, a DCJ operation is applied on the edges labeled with ∗. Orange edges never cross in the intermediate genomes.

Figure 6

(a) A genome M , in orange, with exactly two crossing edges in BP(A, B), with A in green and B in blue. (b) A DCJ operation {pr, sq} → {pq, rs} on M that uncross the edges breaks one AM-cycle in two, keeping the other BM-cycle, meaning that M is not an intermediate genome, as shown in Lemma 2.

Figure 7

Number of AM- and BM-cycles in an AB-cycle of size 2n with n non-crossing M-edges. A-, B- and M -edges are drawn in green, blue and orange, respectively. (a) An AB-cycle of size 2 has one AM- and one BM-cycle. An AB-cycle of size n, shown in (b), has one more AM-cycle than an AB-cycle of size n − 2, with the same number of BM-cycles, shown in (c).

Figure 8

Solving the Guided Intermediate problem for BP(A, B) with two AB-cycles, and guide G = {pq, rs, uv}. At each step, an adjacency from G is taken, and if accepted its vertices and incident edges are removed, and two new edges are added to complete the resulting two smaller AB-cycles. The problem is then recursively solved on the smaller cycles. (a) Initial BP(A, B), where adjacency pq is accepted. (b) Second adjacency rs is also accepted. (c) The adjacency uv covers two components, because it crosses with a previously added adjacency, and it is rejected. (d) In the end of the algorithm, three extra adjacencies (shown as dotted orange edges) are added for each AB-cycle of size 2, since this is the only choice for a non-crossing edge belonging to an intermediate genome M. The final output is then the adjacency set {pq, rs} plus the three adjacencies corresponding to the dotted orange edges.

Figure 9

Percentage of correct adjacencies found by the Homology algorithms, for each tree diameter.

Figure 10

Percentage of correct adjacencies found by the Distance algorithms, for each tree diameter.

Figure 11

Total DCJ tree length for the distance algorithms.

Figure 12

Total DCJ distance between the simulated and reconstructed ancestors for the distance algorithms.