Estimating Metabolic Fluxes Using a Maximum Network Flexibility Paradigm

Abstract

Motivation: Genome-scale metabolic networks can be modeled in a constraint-based fashion. Reaction stoichiometry combined with flux capacity constraints determine the space of allowable reaction rates. This space is often large and a central challenge in metabolic modeling is finding the biologically most relevant flux distributions. A widely used method is flux balance analysis (FBA), which optimizes a biologically relevant objective such as growth or ATP production. Although FBA has proven to be highly useful for predicting growth and byproduct secretion, it cannot predict the intracellular fluxes under all environmental conditions. Therefore, alternative strategies have been developed to select flux distributions that are in agreement with experimental "omics" data, or by incorporating experimental flux measurements. The latter, unfortunately can only be applied to a limited set of reactions and is currently not feasible at the genome-scale. On the other hand, it has been observed that micro-organisms favor a suboptimal growth rate, possibly in exchange for a more "flexible" metabolic network. Instead of dedicating the internal network state to an optimal growth rate in one condition, a suboptimal growth rate is used, that allows for an easier switch to other nutrient sources. A small decrease in growth rate is exchanged for a relatively large gain in metabolic capability to adapt to changing environmental conditions.

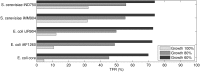
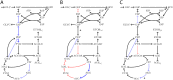
Results: Here, we propose Maximum Metabolic Flexibility (MMF) a computational method that utilizes this observation to find the most probable intracellular flux distributions. By mapping measured flux data from central metabolism to the genome-scale models of Escherichia coli and Saccharomyces cerevisiae we show that i) indeed, most of the measured fluxes agree with a high adaptability of the network, ii) this result can be used to further reduce the space of feasible solutions iii) this reduced space improves the quantitative predictions made by FBA and contains a significantly larger fraction of the measured fluxes compared to the flux space that was reduced by a uniform sampling approach and iv) MMF can be used to select reactions in the network that contribute most to the steady-state flux space. Constraining the selected reactions improves the quantitative predictions of FBA considerably more than adding an equal amount of flux constraints, selected using a more naïve approach. Our method can be applied to any cell type without requiring prior information.

Availability: MMF is freely available as a MATLAB plugin at: http://cs.ru.nl/~wmegchel/mmf.

Fig 1. A toy example of the MMS method.

(A) A toy network with 3 metabolites, connected by 6 reactions. Flux lower- and upper bounds are denoted between brackets. (B) The TFR distribution (relative to the original TFR) for each reaction.

Fig 2. TFR for various genome-scale metabolic reconstructions of E. coli and S. cerevisiae.

The TFR was computed while obtaining a minimum growth output of 60, 80 or 100 percent of the maximum value computed by FBA.

Fig 3. Illustration of the purpose of MMF on four reaction in central carbon metabolism.

(A) The fluxes estimated by pFBA (red) are distant from the measured rates and are also outside the 0.95 TFR range. After applying MMF, the fluxes estimated by pFBA are much closer to the measured rates. Notice that the measured rates are within the 0.95 TFR range, but are generally not captured by the ACHR sampling distribution. (B-D) TFR reduction vs error in scenario 1–3 respectively. The MMF method provides less reduction of the flux ranges, but also has a considerably smaller error rate. The MMF performs best, when the growth rate (scenario 2) and the key exchange fluxes (scenario 3) are constrained.

Fig 4. Flux prediction error for scenario 2.

By first applying MMF, the predictions made by pFBA (MMF + pFBA) improve. The error improves in particular, when the biomass optimization paradigm may not hold (b and d). Furthermore, global optimization of the flexibility works pretty well, except for yeast growing under high oxygen conditions. In this case, yeast produces much biomass and fluxes estimated by pFBA are more accurate. By first applying ACHR, the feasible flux ranges are pruned to heavily, leading to worse flux estimates.

Fig 5. TFR reduction and pFBA improvement of MMF compared to random and “MaxSpan” selection on the S. cerevisiae iMM904 model (high oxygen).

(A) The MMF method selects flux measurements that provide a larger reduction of the flux ranges compared to the MaxSpan or random measurements. (B) Fluxes predicted by pFBA obtain the smallest errors when the reactions selected by MMF are measured.

Fig 6. Effect of flux selection by MMF for explained with a network reconstruction of S. cerevisiae central metabolism.

Red arrows denote overestimated fluxes by pFBA, compared to the measured data. Blue arrows denote underestimated fluxes. Using subsequent measurements in glycolysis (g3p -> pep) and the TCA cycle (succinyl-coA -> succinate), the pFBA estimates are much closer to the measured fluxes.