Biological Effects of Low-Frequency Shear Strain: Physical Descriptors
- PMID: 26458790
- PMCID: PMC4666766
- DOI: 10.1016/j.ultrasmedbio.2015.08.016
Biological Effects of Low-Frequency Shear Strain: Physical Descriptors
Abstract
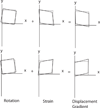
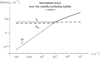
Biological effects of megahertz-frequency diagnostic ultrasound are thoroughly monitored by professional societies throughout the world. A corresponding, thorough, quantitative evaluation of the archival literature on the biological effects of low-frequency vibration is needed. Biological effects, of course, are related directly to what those exposures do physically to the tissue-specifically, to the shear strains that those sources produce in the tissues. Instead of the simple compressional strains produced by diagnostic ultrasound, realistic sources of low-frequency vibration produce both fast (∼1,500 m/s) and slow (1-10 m/s) waves, each of which may have longitudinal and transverse shear components. Part 1 of this series illustrates the resulting strains, starting with those produced by longitudinally and transversely oscillating planes, through monopole and dipole sources of fast waves and, finally, to the case of a sphere moving in translation-the simplest model of the fields produced by realistic sources.
Keywords: Acoustic dipole; Acoustic monopole; Biological effects; Low-frequency shear strain; Low-frequency vibration; Tactile perception; Transverse and longitudinal shear waves.
Copyright © 2016 World Federation for Ultrasound in Medicine & Biology. Published by Elsevier Inc. All rights reserved.
Figures
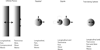
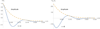










References
-
- Békésy Gv. Über die Vibrationsempfindung. Akustische Zeitschrift. 1939;4:315–334.
-
- Bell J, Bolanowski S, Holmes MH. The structure and function of Pacinian corpuscles: a review. Progress in neurobiology. 1994;42:79–128. - PubMed
-
- Brisben AJ, Hsiao SS, Johnson KO. Detection of vibration transmitted through an object grasped in the hand. Journal of neurophysiology. 1999;81:1548–1558. - PubMed
-
- Carstensen E, Parker KJ. Oestreicher and elastography. J Acoust Soc Am. (in press). - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

