Precision of maximum likelihood estimation in adaptive designs

Abstract

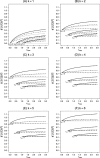
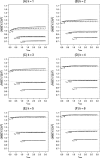
There has been increasing interest in trials that allow for design adaptations like sample size reassessment or treatment selection at an interim analysis. Ignoring the adaptive and multiplicity issues in such designs leads to an inflation of the type 1 error rate, and treatment effect estimates based on the maximum likelihood principle become biased. Whereas the methodological issues concerning hypothesis testing are well understood, it is not clear how to deal with parameter estimation in designs were adaptation rules are not fixed in advanced so that, in practice, the maximum likelihood estimate (MLE) is used. It is therefore important to understand the behavior of the MLE in such designs. The investigation of Bias and mean squared error (MSE) is complicated by the fact that the adaptation rules need not be fully specified in advance and, hence, are usually unknown. To investigate Bias and MSE under such circumstances, we search for the sample size reassessment and selection rules that lead to the maximum Bias or maximum MSE. Generally, this leads to an overestimation of Bias and MSE, which can be reduced by imposing realistic constraints on the rules like, for example, a maximum sample size. We consider designs that start with k treatment groups and a common control and where selection of a single treatment and control is performed at the interim analysis with the possibility to reassess each of the sample sizes. We consider the case of unlimited sample size reassessments as well as several realistically restricted sample size reassessment rules.

Keywords: adaptive designs; maximum likelihood estimation; sample size reassessment; treatment selection.

Figure 1

Standardized maximum Bias as a function of r _max for r _min=0, 0.5, and 1. Values are given for a number of k = 1 to 6 treatments in panels (A) to (F). Within one panel the standardized maximum Bias is shown for different restrictions on the sample size reassessment rule: flexible second‐to‐first‐stage‐ratios (solid lines), equal second‐to‐first‐stage ratios (dotted lines), restricting $r_1\ge r_0$ (dot‐dashed lines), and fixing the control (dashed lines). The gray horizontal line shows the standardized Bias for a fixed‐size‐sample test with post‐trial selection.

Figure 2

Standardized maximum root mean squared error (RMSE) as a function of r _max for r _min=0, 0.5, and 1. Values are given for a number of k = 1 to 6 treatments in panels (A) to (F). Within one panel, the standardized maximum RMSE is shown for different restrictions on the sample‐size reassessment rule: flexible second‐to‐first‐stage ratios (solid lines), equal second‐to‐first‐stage ratios (dotted lines), restricting $r_1\ge r_0$ (dot‐dashed lines), and fixing the control (dashed lines). The solid gray horizontal line shows the standardized maximum RMSE for a fixed‐size‐sample test with post‐trial selection. The dashed gray horizontal line shows the standardized RMSE of a fixed‐sample‐size test when selecting the treatment with the maximum effect at the end.

Figure 3

Standardized maximum Bias, panel (A), and the standardized maximum root mean squared error, panel (B), as a function of the timing t of the interim analysis for k = 1 to 6 treatments compared with one common control for the case of full (solid black lines) and restricted reshuffling (dashed black‐lines). For comparison, the standardized Bias and root mean squared error are given for an adaptive design with treatment selection and a sample size of (1 − t)n _g(k + 1)/2 in the second stage (gray lines).

Figure A1

Subsets of the interim outcome of treatment and control (z ₀,z ₁) to be used for evaluating the worst case conditional Bias (first row) and the worst case conditional MSE (second row). Subsets are given for flexible second‐to‐first‐stage ratios (first column) and the case of reshuffling (second column).