Unconstrained muscle-tendon workloops indicate resonance tuning as a mechanism for elastic limb behavior during terrestrial locomotion

Abstract

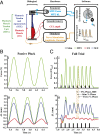
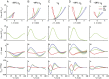
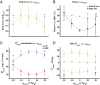
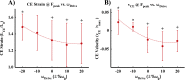
In terrestrial locomotion, there is a missing link between observed spring-like limb mechanics and the physiological systems driving their emergence. Previous modeling and experimental studies of bouncing gait (e.g., walking, running, hopping) identified muscle-tendon interactions that cycle large amounts of energy in series tendon as a source of elastic limb behavior. The neural, biomechanical, and environmental origins of these tuned mechanics, however, have remained elusive. To examine the dynamic interplay between these factors, we developed an experimental platform comprised of a feedback-controlled servo-motor coupled to a biological muscle-tendon. Our novel motor controller mimicked in vivo inertial/gravitational loading experienced by muscles during terrestrial locomotion, and rhythmic patterns of muscle activation were applied via stimulation of intact nerve. This approach was based on classical workloop studies, but avoided predetermined patterns of muscle strain and activation-constraints not imposed during real-world locomotion. Our unconstrained approach to position control allowed observation of emergent muscle-tendon mechanics resulting from dynamic interaction of neural control, active muscle, and system material/inertial properties. This study demonstrated that, despite the complex nonlinear nature of musculotendon systems, cyclic muscle contractions at the passive natural frequency of the underlying biomechanical system yielded maximal forces and fractions of mechanical work recovered from previously stored elastic energy in series-compliant tissues. By matching movement frequency to the natural frequency of the passive biomechanical system (i.e., resonance tuning), muscle-tendon interactions resulting in spring-like behavior emerged naturally, without closed-loop neural control. This conceptual framework may explain the basis for elastic limb behavior during terrestrial locomotion.

Keywords: elastic limb behavior; muscle-tendon mechanics; neural control; resonance; terrestrial locomotion.

Fig. 1.

(A) Schematic of bio-robotic system. (B) Force (i) and displacement (ii) data from a passive pluck condition. Note that patterns of force and displacement are cyclic. (C) Full force (i) and displacement (ii) data representative of the ${\text{ω}}_0$ condition from this study. Note that the system rapidly stabilizes and reaches steady state. The convention used to define muscle stimulation onset and peak force phase is annotated between C, i and ii.

Fig. S1.

An annotated photograph of an experimental preparation. Colors used correspond to those of the figure schematic in Fig. 1A to allow for easy comparisons between components of the MTU.

Fig. 2.

A representative dataset from a single preparation showing (i) mean workloop, (ii) force ± SE, (iii) ΔL ± SE, and (iv) mechanical power ± SE output dynamics for the (A) $-20{\text{\%ω}}_0$, (B) $-10{\text{\%ω}}_0$, (C) ${\text{ω}}_0$, (D) $+10{\text{\%ω}}_0$, and (E) +20%${\text{ω}}_0$ conditions. All mean/SE data are based on the last four stimulation cycles from each condition. Note that SE bounds are generally small, indicating steady-state behavior from cycle to cycle. Also note progression from detuned to tuned between ${\text{ω}}_{\text{Drive}}$ of $-20{\text{\%ω}}_0$ and ${\text{ω}}_0$ (A, i–iv to C, i–iv), and back to detuned again in the +20% condition (C, i–iv to E, i–iv). All cycles begin (0%) and end (100%) with muscle stimulation onset.

Fig. 3.

Mean ± SD data for (A) normalized peak force, (B) peak force and muscle stimulation phase, (C) contribution of overall positive mechanical work coming from muscle (CE) vs. tendon (SEE), and (D) MTU positive (▴), negative (▾), and net (▪) average mechanical power over a cycle of stimulation. All power values are reported in units of Watts per kilogram of muscle mass. In all figures, conditions significantly different (post hoc paired t test, P < 0.05) from ${\text{ω}}_0$ and/or the global observed maximum/minimum are indicated by a superscript of * and +/#, respectively, for these metrics.

Fig. S2.

Mean ± SD values of (A) normalized CE strain and (B) normalized CE velocity at peak force. In all figures, statistically significant pairwise comparisons (P < 0.05) to the ${\text{ω}}_0$ condition are annotated with an asterisk. In both plots, the global maximum mean value was not the ${\text{ω}}_0$ condition, so pairwise comparisons to the global maximum were also performed. Conditions found to be significantly different from the global maximum are indicated by a plus sign.

Fig. S3.

Comparisons of mean ± SD values from this study (Left) and human hopping studies (Right) for peak MTU force (A and B), MTU average positive (▴), negative (▾), and net (▪) mechanical power (C and D), CE/SEE power sharing (E and F), average metabolic rate (G and H), and MTU apparent efficiency (I and J). In figures pertaining to this study (Left), statistically significant pairwise comparisons (P <0.05) to the ${\text{ω}}_0$ condition are annotated with an asterisk. If the global max/min mean value was not the ${\text{ω}}_0$ condition, pairwise comparisons to the global maximum (+) or minimum (#) value were performed depending on which extreme is appropriate for a given metric. For human data (Right), the resonant condition is unknown, and pairwise comparisons are performed relative to observed maximum (+) or minimum (#) depending on the metric examined. All power data reported here are in Watts per kilograms of muscle mass for the in vitro preparation (C and G), and Watts per kilogram of body mass for human data (D and H).