Automated generation of node-splitting models for assessment of inconsistency in network meta-analysis
- PMID: 26461181
- PMCID: PMC5057346
- DOI: 10.1002/jrsm.1167
Automated generation of node-splitting models for assessment of inconsistency in network meta-analysis
Abstract
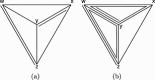
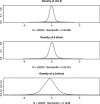
Network meta-analysis enables the simultaneous synthesis of a network of clinical trials comparing any number of treatments. Potential inconsistencies between estimates of relative treatment effects are an important concern, and several methods to detect inconsistency have been proposed. This paper is concerned with the node-splitting approach, which is particularly attractive because of its straightforward interpretation, contrasting estimates from both direct and indirect evidence. However, node-splitting analyses are labour-intensive because each comparison of interest requires a separate model. It would be advantageous if node-splitting models could be estimated automatically for all comparisons of interest. We present an unambiguous decision rule to choose which comparisons to split, and prove that it selects only comparisons in potentially inconsistent loops in the network, and that all potentially inconsistent loops in the network are investigated. Moreover, the decision rule circumvents problems with the parameterisation of multi-arm trials, ensuring that model generation is trivial in all cases. Thus, our methods eliminate most of the manual work involved in using the node-splitting approach, enabling the analyst to focus on interpreting the results.
Keywords: Bayesian modelling; meta-analysis; mixed treatment comparisons; model generation; network meta-analysis; node splitting.
© 2015 The Authors Research Synthesis Methods Published by John Wiley & Sons Ltd.
Figures


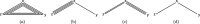


References
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

