Transcriptional Bursting in Gene Expression: Analytical Results for General Stochastic Models
- PMID: 26474290
- PMCID: PMC4608583
- DOI: 10.1371/journal.pcbi.1004292
Transcriptional Bursting in Gene Expression: Analytical Results for General Stochastic Models
Abstract
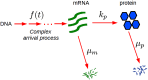
Gene expression in individual cells is highly variable and sporadic, often resulting in the synthesis of mRNAs and proteins in bursts. Such bursting has important consequences for cell-fate decisions in diverse processes ranging from HIV-1 viral infections to stem-cell differentiation. It is generally assumed that bursts are geometrically distributed and that they arrive according to a Poisson process. On the other hand, recent single-cell experiments provide evidence for complex burst arrival processes, highlighting the need for analysis of more general stochastic models. To address this issue, we invoke a mapping between general stochastic models of gene expression and systems studied in queueing theory to derive exact analytical expressions for the moments associated with mRNA/protein steady-state distributions. These results are then used to derive noise signatures, i.e. explicit conditions based entirely on experimentally measurable quantities, that determine if the burst distributions deviate from the geometric distribution or if burst arrival deviates from a Poisson process. For non-Poisson arrivals, we develop approaches for accurate estimation of burst parameters. The proposed approaches can lead to new insights into transcriptional bursting based on measurements of steady-state mRNA/protein distributions.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

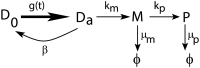


Similar articles
-
Applications of Little's Law to stochastic models of gene expression.Phys Rev E Stat Nonlin Soft Matter Phys. 2010 Aug;82(2 Pt 1):021901. doi: 10.1103/PhysRevE.82.021901. Epub 2010 Aug 3. Phys Rev E Stat Nonlin Soft Matter Phys. 2010. PMID: 20866831
-
Connecting protein and mRNA burst distributions for stochastic models of gene expression.Phys Biol. 2011 Aug;8(4):046001. doi: 10.1088/1478-3975/8/4/046001. Epub 2011 Apr 13. Phys Biol. 2011. PMID: 21490380
-
Exact protein distributions for stochastic models of gene expression using partitioning of Poisson processes.Phys Rev E Stat Nonlin Soft Matter Phys. 2013 Apr;87(4):042720. doi: 10.1103/PhysRevE.87.042720. Epub 2013 Apr 26. Phys Rev E Stat Nonlin Soft Matter Phys. 2013. PMID: 23679462
-
Stochastic and delayed stochastic models of gene expression and regulation.Math Biosci. 2010 Jan;223(1):1-11. doi: 10.1016/j.mbs.2009.10.007. Epub 2009 Oct 31. Math Biosci. 2010. PMID: 19883665 Review.
-
Solving stochastic gene-expression models using queueing theory: A tutorial review.Biophys J. 2024 May 7;123(9):1034-1057. doi: 10.1016/j.bpj.2024.04.004. Epub 2024 Apr 9. Biophys J. 2024. PMID: 38594901 Free PMC article. Review.
Cited by
-
Queuing Models of Gene Expression: Analytical Distributions and Beyond.Biophys J. 2020 Oct 20;119(8):1606-1616. doi: 10.1016/j.bpj.2020.09.001. Epub 2020 Sep 9. Biophys J. 2020. PMID: 32966761 Free PMC article.
-
Buffering and Amplifying Transcriptional Noise During Cell Fate Specification.Front Genet. 2018 Nov 29;9:591. doi: 10.3389/fgene.2018.00591. eCollection 2018. Front Genet. 2018. PMID: 30555516 Free PMC article. Review.
-
Profiling of Invasive Breast Carcinoma Circulating Tumour Cells-Are We Ready for the 'Liquid' Revolution?Cancers (Basel). 2019 Jan 25;11(2):143. doi: 10.3390/cancers11020143. Cancers (Basel). 2019. PMID: 30691008 Free PMC article. Review.
-
Mixture distributions in a stochastic gene expression model with delayed feedback: a WKB approximation approach.J Math Biol. 2020 Jul;81(1):343-367. doi: 10.1007/s00285-020-01512-y. Epub 2020 Jun 24. J Math Biol. 2020. PMID: 32583030 Free PMC article.
-
A transcriptional cycling model recapitulates chromatin-dependent features of noisy inducible transcription.PLoS Comput Biol. 2022 Sep 9;18(9):e1010152. doi: 10.1371/journal.pcbi.1010152. eCollection 2022 Sep. PLoS Comput Biol. 2022. PMID: 36084132 Free PMC article.
References
-
- Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297(5584):1183–1186. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

