Route to Topological Superconductivity via Magnetic Field Rotation
- PMID: 26477669
- PMCID: PMC4609968
- DOI: 10.1038/srep15302
Route to Topological Superconductivity via Magnetic Field Rotation
Abstract
The verification of topological superconductivity has become a major experimental challenge. Apart from the very few spin-triplet superconductors with p-wave pairing symmetry, another candidate system is a conventional, two-dimensional (2D) s-wave superconductor in a magnetic field with a sufficiently strong Rashba spin-orbit coupling. Typically, the required magnetic field to convert the superconductor into a topologically non-trivial state is however by far larger than the upper critical field H(c2), which excludes its realization. In this article, we argue that this problem can be overcome by rotating the magnetic field into the superconducting plane. We explore the character of the superconducting state upon changing the strength and the orientation of the magnetic field and show that a topological state, established for a sufficiently strong out-of-plane magnetic field, indeed extends to an in-plane field orientation. We present a three-band model applicable to the superconducting interface between LaAlO3 and SrTiO3, which should fulfil the necessary conditions to realize a topological superconductor.
Figures
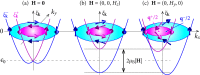

 ,
,  and Δ is fixed to 0.1 t), the total Berry curvature integrates to zero over the Brillouin zone. (b) In the topological situation (B) (see main text,
and Δ is fixed to 0.1 t), the total Berry curvature integrates to zero over the Brillouin zone. (b) In the topological situation (B) (see main text,  and
and  ), the Berry curvature integrates to 2πC = 4π over the Brillouin zone.
), the Berry curvature integrates to 2πC = 4π over the Brillouin zone.
 . For such low densities, a large interaction strength V is required to obtain a reasonably large order parameter. For each value of |H|, q− = (q, 0) is obtained by minimizing the free energy. The red circles indicate the magnetic field strength above which a finite COMM q ≠ 0 is present.
. For such low densities, a large interaction strength V is required to obtain a reasonably large order parameter. For each value of |H|, q− = (q, 0) is obtained by minimizing the free energy. The red circles indicate the magnetic field strength above which a finite COMM q ≠ 0 is present.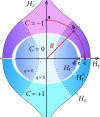

 , (b)
, (b)  , (c)
, (c)  , and
, and  . The self-consistently calculated order parameters
. The self-consistently calculated order parameters  and COMMs q− are (a)
and COMMs q− are (a)  , (b)
, (b)  , and (c)
, and (c)  . (d,e) illustrate the crossover regime
. (d,e) illustrate the crossover regime  : (d)
: (d)  and
and  , and (e)
, and (e)  and
and  . The black arrows in (d) indicate the partial occupation of states originating from the
. The black arrows in (d) indicate the partial occupation of states originating from the  -band. The opacity of each point encodes the weight with which the corresponding state contributes to the density of states.
-band. The opacity of each point encodes the weight with which the corresponding state contributes to the density of states.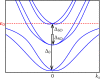
 (red dashed line), the Fermi energy should be at the degeneracy point of the upper, Rashba-like doublet. The parameters are here:
(red dashed line), the Fermi energy should be at the degeneracy point of the upper, Rashba-like doublet. The parameters are here:  , Δ0 = t,
, Δ0 = t,  .
.References
-
- Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
-
- Sau J. D., Lutchyn R. M., Tewari S. & Das Sarma S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 1–4 (2010). - PubMed
-
- Alicea J. Majorana fermions in a tunable semiconductor device. Phys. Rev. B 81, 125318 1–10 (2010).
-
- Sato M. & Fujimoto S. Topological phases of noncentrosymmetric superconductors: edge states, Majorana fermions, and non-Abelian statistics. Phys. Rev. B 79, 094504 1–16 (2009).
-
- Sato M., Takahashi Y. & Fujimoto S. Non-Abelian topological order in s-wave superfluids of ultracold fermionic atoms. Phys. Rev. Lett. 103, 020401 1–4 (2009). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

