The Scaling of Human Contacts and Epidemic Processes in Metapopulation Networks
- PMID: 26478209
- PMCID: PMC4609962
- DOI: 10.1038/srep15111
The Scaling of Human Contacts and Epidemic Processes in Metapopulation Networks
Abstract
We study the dynamics of reaction-diffusion processes on heterogeneous metapopulation networks where interaction rates scale with subpopulation sizes. We first present new empirical evidence, based on the analysis of the interactions of 13 million users on Twitter, that supports the scaling of human interactions with population size with an exponent γ ranging between 1.11 and 1.21, as observed in recent studies based on mobile phone data. We then integrate such observations into a reaction- diffusion metapopulation framework. We provide an explicit analytical expression for the global invasion threshold which sets a critical value of the diffusion rate below which a contagion process is not able to spread to a macroscopic fraction of the system. In particular, we consider the Susceptible-Infectious-Recovered epidemic model. Interestingly, the scaling of human contacts is found to facilitate the spreading dynamics. This behavior is enhanced by increasing heterogeneities in the mobility flows coupling the subpopulations. Our results show that the scaling properties of human interactions can significantly affect dynamical processes mediated by human contacts such as the spread of diseases, ideas and behaviors.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
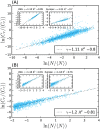
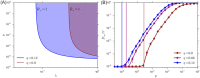
 , and μ = 0.3. (B) Simulated global attack rate D∞/V as a function of the mobility rate p for different values of the contact scaling exponent η = 0, 0.06, 0.12 and λ = 0.35. Vertical lines indicate the critical threshold value pc calculated by setting R* = 1 in Eq. 5. Each point is averaged over at least 2 × 103 simulations. Error bars correspond to the standard error of the mean.
, and μ = 0.3. (B) Simulated global attack rate D∞/V as a function of the mobility rate p for different values of the contact scaling exponent η = 0, 0.06, 0.12 and λ = 0.35. Vertical lines indicate the critical threshold value pc calculated by setting R* = 1 in Eq. 5. Each point is averaged over at least 2 × 103 simulations. Error bars correspond to the standard error of the mean.
Similar articles
-
Invasion threshold in heterogeneous metapopulation networks.Phys Rev Lett. 2007 Oct 5;99(14):148701. doi: 10.1103/PhysRevLett.99.148701. Epub 2007 Oct 5. Phys Rev Lett. 2007. PMID: 17930732
-
Invasion threshold in structured populations with recurrent mobility patterns.J Theor Biol. 2012 Jan 21;293:87-100. doi: 10.1016/j.jtbi.2011.10.010. Epub 2011 Oct 19. J Theor Biol. 2012. PMID: 22019505 Free PMC article.
-
Epidemic modeling in metapopulation systems with heterogeneous coupling pattern: theory and simulations.J Theor Biol. 2008 Apr 7;251(3):450-67. doi: 10.1016/j.jtbi.2007.11.028. Epub 2007 Nov 29. J Theor Biol. 2008. PMID: 18222487
-
Modeling epidemics: A primer and Numerus Model Builder implementation.Epidemics. 2018 Dec;25:9-19. doi: 10.1016/j.epidem.2018.06.001. Epub 2018 Jul 13. Epidemics. 2018. PMID: 30017895 Review.
-
Epidemionics: from the host-host interactions to the systematic analysis of the emergent macroscopic dynamics of epidemic networks.Virulence. 2010 Jul-Aug;1(4):338-49. doi: 10.4161/viru.1.4.12196. Virulence. 2010. PMID: 21178467 Review.
Cited by
-
Intervention threshold for epidemic control in susceptible-infected-recovered metapopulation models.Phys Rev E. 2019 Aug;100(2-1):022302. doi: 10.1103/PhysRevE.100.022302. Phys Rev E. 2019. PMID: 31574659 Free PMC article.
-
Local rabies transmission and regional spatial coupling in European foxes.PLoS One. 2020 May 29;15(5):e0220592. doi: 10.1371/journal.pone.0220592. eCollection 2020. PLoS One. 2020. PMID: 32469961 Free PMC article.
-
Connecting Mobility to Infectious Diseases: The Promise and Limits of Mobile Phone Data.J Infect Dis. 2016 Dec 1;214(suppl_4):S414-S420. doi: 10.1093/infdis/jiw273. J Infect Dis. 2016. PMID: 28830104 Free PMC article. Review.
-
A targeted e-learning approach for keeping universities open during the COVID-19 pandemic while reducing student physical interactions.PLoS One. 2021 Apr 8;16(4):e0249839. doi: 10.1371/journal.pone.0249839. eCollection 2021. PLoS One. 2021. PMID: 33831082 Free PMC article.
-
Asymptotic theory of time-varying social networks with heterogeneous activity and tie allocation.Sci Rep. 2016 Oct 24;6:35724. doi: 10.1038/srep35724. Sci Rep. 2016. PMID: 27774998 Free PMC article.
References
-
- Easley D. & Kleinberg J.. Networks, Crowds, and Markets: Reasoning about a Highly Connected World. Cambridge University Press (2010).
-
- Keeling M. J. & Rohani P.. Modeling infectious diseases in humans and animals. Princeton Univeristy Press (2008).
-
- Newman M. E. J.. Networks, an Introduction. Oxford University Press (2010).
-
- Barrat A., Barthélemy M. & Vespignani A.. Dynamical Processes on Complex Networks. Cambridge University Press (2008).
-
- Cohen R. & Havlin S.. Complex Networks: Structure, Robustness and Function. Cambridge University Press, Cambridge (2010).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

