Anomalous segregation dynamics of self-propelled particles

Abstract

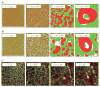
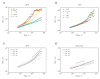
A number of novel experimental and theoretical results have recently been obtained on active soft matter, demonstrating the various interesting universal and anomalous features of this kind of driven systems. Here we consider the adhesion difference-driven segregation of actively moving units, a fundamental but still poorly explored aspect of collective motility. In particular, we propose a model in which particles have a tendency to adhere through a mechanism which makes them both stay in touch and synchronize their direction of motion - but the interaction is limited to particles of the same kind. The calculations corresponding to the related differential equations can be made in parallel, thus a powerful GPU card allows large scale simulations. We find that in a very large system of particles, interacting without explicit alignment rule, three basic segregation regimes seem to exist as a function of time: i) at the beginning the time dependence of the correlation length is analogous to that predicted by the Cahn-Hillard theory, ii) next rapid segregation occurs characterized with a separation of the different kinds of units being faster than any previously suggested speed, finally, iii) the growth of the characteristic sizes in the system slows down due to a new regime in which self-confined, rotating, splitting and re-joining clusters appear. Our results can explain recent observations of segregating tissue cells in vitro.

Keywords: cell segregation; dynamical exponents; nonequilibrium; spp model.

FIG. 1

Morphologies characterizing the segregation of a SPP mixture at 50:50 (a) and at red:green = 40:60 (b) coverage ratios. Red particles are more motile than green particles (see Table I, N = 10⁵, L = L₀ = 100). White areas are devoid of particles – uniform clusters can achieve higher local cell density than areas where the two particle types are intermixed and their movement is less correlated. In the final state of the simulation the red cluster rotates (see supplemental material). As a comparison, we show characteristic images from the experiment of [18] (c). Time unit t corresponds to the time needed for an SPP particle or cell to move a distance that is equal to the average particle/cell size.

FIG. 2

An SPP system can segregate much faster than a similar system containing noise-driven (Brownian) particles. In Brownian simulations the characteristic linear size of the segregated domains grows according to the Cahn-Hilliard behavior. In contrast, the SPP system with steering rule (7) exhibits a regime where the average cluster size is proportional to time. Fast segregation is also observed in simulations where all particles have identical properties (values characterizing red particles in Table I), and the segregation is driven only by the lack of adhesion between red and green particles (inset, noise=6.3°, coverage: 70%). Persistent random motility without the specific steering rule (7) also exhibits Cahn-Hilliard coarsening. The solid lines are guides to the eye. Spatial scale unit is the mean particle diameter, temporal unit is the time an SPP needs to move a unit distance. Error bars represent standard error of the mean (≤ n ≤ 12).

FIG. 3

Cluster size dynamics for various model parameter values. A: Better steering quality (decreased noise) yields earlier and faster segregation. The transition between the fast (z ≈ 1) and slow (z ≈ 1/3) mechanism is sudden (elicited by a 10% change in the noise parameter) and is coincident with the transition between a long-range ordered (rotating) and a locally ordered, but globally disordered system. In the transient regime (red symbols) the velocity correlation length is still smaller than the system size, yet the segregation is much faster than the Cahn-Hilliard behavior. B: Maximal cluster size is limited by the system size. For larger systems the linear growth regime is extended. C: When the coverage ratio differs from 1:1, the segregation is slower than the linear growth shown in panels A and B, yet it is still faster than the Cahn-Hilliard behavior. D: As a comparison, noise driven particle system exhibit Cahn-Hilliard segregation with z ≈ 1/3 for 1:1 coverage ratio and z ≈ 1/4 otherwise.

FIG. 4

Directions of particle movements at various stages of the segregation process. Panels (A) and (B) depict color coded velocity directions of one particle type, the green particles, shown in Fig 1 at 50:50 (A) and red:green = 40:60 (B) coverage ratios. C: Velocity directions of both red and green particles within the system shown in panel A. The abrupt change of motion direction at segregation boundaries (asterisks) indicates that segregated cell groups can slide against each other. D: Heading directions in the same snapshot shown in panel C. Gray colors indicate that heading directions are less correlated locally than actual displacements are.