Estimating Tumor Growth Rates In Vivo

Abstract

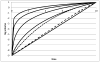
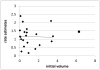
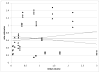
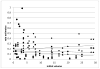
In this paper, we develop methods for inferring tumor growth rates from the observation of tumor volumes at two time points. We fit power law, exponential, Gompertz, and Spratt’s generalized logistic model to five data sets. Though the data sets are small and there are biases due to the way the samples were ascertained, there is a clear sign of exponential growth for the breast and liver cancers, and a 2/3’s power law (surface growth) for the two neurological cancers.

Figure 1

Correction factors f(V) for the models plotted against log(V). The Gompertz is the straight line of diamonds, Spratt are the squares, while power laws 2/3, 0.8 and 0.9 are in decreasing order the curves marked with triangles.

Figure 2

Comparison of log₁₀ V (t) for our models. All start with one cell, V (0) = 10⁻⁹ cm³. Rates are chosen so that V (10) = 10 cm³. The solid lines in decreasing order are power laws α = 0.5, 2/3, 0.8, 0.9. The exponential is the straight line −9 + t. The dashed lines are Gompertz (larger) and Spratt (close to exponential).

Figure 3

Heuser data set: Exponential growth rate estimates plotted versus initial volume. The tumor indicated by the square was not used to compute the regression line.

Figure 4

Exponential (squares) and Spratt (diamonds) rate estimates for the Saito data set, and the corresponding regression lines that have slopes 0.0488 and 0.1337. As to be expected the Spratt rate estimate is larger, and the discrepancy increases with the initial size of the tumor.

Figure 5

Nakajima data set. The diamonds are the four points we discarded. Also shown are the regression line fits for the entire data (slope 0.1131) and reduced data sets (slope 0.0274). The three diamonds with initial volume > 10 cm³ are responsible for the large increase in slope.

Figure 6

Exponential rate estimates for the Laasonen and Troupp [13] data, showing the large influence of the two points with initial volume > 7 cm³.

Figure 7

Rate estimates for the power laws 0.5 (circle), 2/3 (diamond), and 0.8 (triangle) for the Laasonen and Troup data plotted versus initial tumor size V₁, as well as the three least squares lines, which have slopes 0.0855, −6 × 10⁻⁶, and −0.0711. Note that in most cases (but not all) the rate estimate decreases as the power increases.

Figure 8

Rate estimates for the power laws 0.5 (diamond), 2/3 (square), and 0.8 (triangle) for the Nakamura data plotted versus initial tumor size V₁, as well as the three regression lines, which which have slopes 0.0028, −0.0010, and −0.0027. The circles are the 0.5 rate estimates for the five tumors we have excluded.

Figure 9

Variability in the logarithm of the rate estimates centered by subtracting the mean of the logarithms. From top to bottom we have the exponential rate estimates for Heuser, Saito, and Nakajima, followed by the 2/3 power law estimates for Laasonen and Tropp, and Nakamura.