An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging
- PMID: 26481672
- PMCID: PMC4692656
- DOI: 10.1016/j.neuroimage.2015.10.019
An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging
Abstract
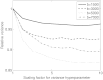
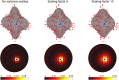
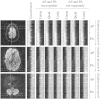
In this paper we describe a method for retrospective estimation and correction of eddy current (EC)-induced distortions and subject movement in diffusion imaging. In addition a susceptibility-induced field can be supplied and will be incorporated into the calculations in a way that accurately reflects that the two fields (susceptibility- and EC-induced) behave differently in the presence of subject movement. The method is based on registering the individual volumes to a model free prediction of what each volume should look like, thereby enabling its use on high b-value data where the contrast is vastly different in different volumes. In addition we show that the linear EC-model commonly used is insufficient for the data used in the present paper (high spatial and angular resolution data acquired with Stejskal-Tanner gradients on a 3T Siemens Verio, a 3T Siemens Connectome Skyra or a 7T Siemens Magnetome scanner) and that a higher order model performs significantly better. The method is already in extensive practical use and is used by four major projects (the WU-UMinn HCP, the MGH HCP, the UK Biobank and the Whitehall studies) to correct for distortions and subject movement.
Keywords: Diffusion; Eddy current; Movement; Registration; Susceptibility.
Copyright © 2015 The Authors. Published by Elsevier Inc. All rights reserved.
Figures

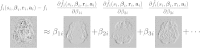

References
-
- Alexander A.L., Tsuruda J.S., Parker D.L. Elimination of eddy current artifacts in diffusion weighted echo-planar images: the use of bipolar gradients. Magn. Reson. Med. 1997;38(2):1016–1021. - PubMed
-
- Alexander A.L., Wu Y.-C., Venkat P.C. Hybrid diffusion imaging (HYDI) Magn. Reson. Med. 2006;38(2):1016–1021. - PubMed
-
- Andersson J.L.R. How to obtain high-accuracy image registration: application to movement correction of dynamic positron emission tomography data. Eur. J. Nucl. Med. 1998;25:575–586. - PubMed
-
- Andersson J.L.R., Skare S. A model-based method for retrospective correction of geometric distortions in diffusion-weighted EPI. NeuroImage. 2002;16:177–199. - PubMed
-
- Andersson J.L.R., Skare S. Chapter 17: Image distortion and its correction in diffusion MRI. In: Jones D.K., editor. Diffusion MRI: Theory, Methods, and Applications. Oxford University Press; Oxford, United Kingdom: 2011. pp. 285–302.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

