Conditional robustness analysis for fragility discovery and target identification in biochemical networks and in cancer systems biology

Abstract

Background: The study of cancer therapy is a key issue in the field of oncology research and the development of target therapies is one of the main problems currently under investigation. This is particularly relevant in different types of tumor where traditional chemotherapy approaches often fail, such as lung cancer.

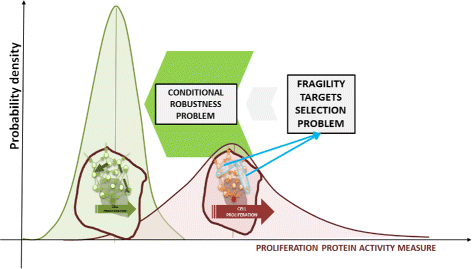
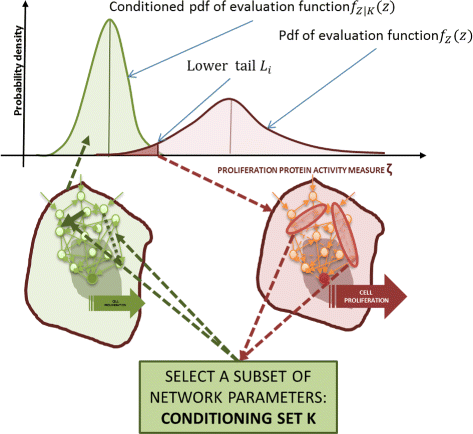
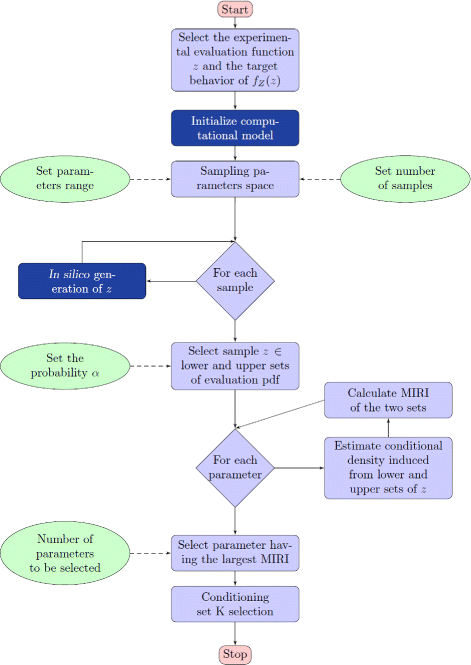
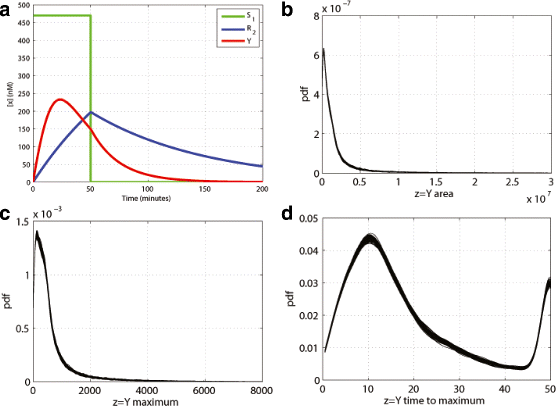
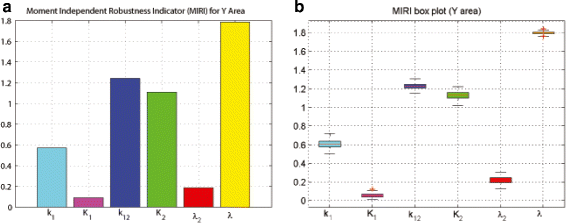
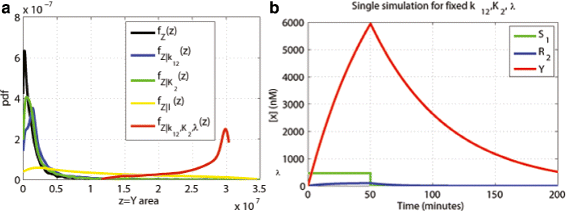
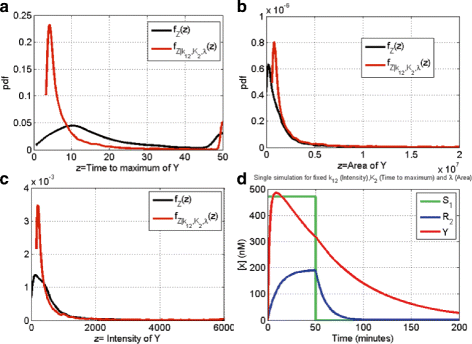
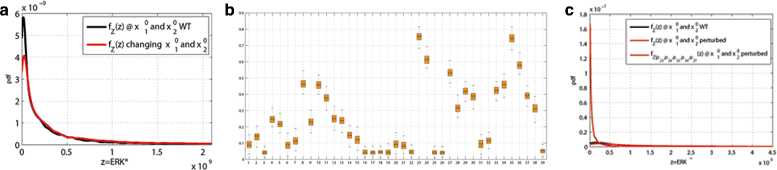
Results: We started from the general definition of robustness introduced by Kitano and applied it to the analysis of dynamical biochemical networks, proposing a new algorithm based on moment independent analysis of input/output uncertainty. The framework utilizes novel computational methods which enable evaluating the model fragility with respect to quantitative performance measures and parameters such as reaction rate constants and initial conditions. The algorithm generates a small subset of parameters that can be used to act on complex networks and to obtain the desired behaviors. We have applied the proposed framework to the EGFR-IGF1R signal transduction network, a crucial pathway in lung cancer, as an example of Cancer Systems Biology application in drug discovery. Furthermore, we have tested our framework on a pulse generator network as an example of Synthetic Biology application, thus proving the suitability of our methodology to the characterization of the input/output synthetic circuits.

Conclusions: The achieved results are of immediate practical application in computational biology, and while we demonstrate their use in two specific examples, they can in fact be used to study a wider class of biological systems.

Fig. 1

Cancer cell proliferation. Green cells are normal cells and red cells are tumor cells. The proliferation activity of normal and tumor cells can be measured looking at the activation of a proliferation protein, which is driven by a complex network based on protein interactions. In a population of cells the proliferation activity can be described by means of probability density for the proliferation protein; e.g., phosphorylated form of the extracellular signal-regulated kinase (ERK). The plots at the bottom show an example of probability density of a proliferation indicator in tumor (red line) and normal cells (green line), respectively

Fig. 2

Problem formulation. The fragility problem in the oncology context is related to the cancer cells signaling network, and the goal is to reduce the cell proliferation attitude acting in few target molecules. The problem is related to the conditional robustness problem, namely the problem of shifting the probability density function of a proliferation signal in cancer cells toward the density describing the normal cells

Fig. 3

General problem formulation of conditional robustness. The problem addressed in this paper is that of selecting a suitable conditioning set K (a proper subset of parameter vector and the corresponding values), achieving a conditional probability density function f _Z|K(z) having values of the output function in a given lower set L _i

Fig. 4

The flowchart of the Conditional Robustness Algorithm (CRA). The CRA has four input values to be set (green ellipses in the diagram) and go through six steps

Fig. 5

Pulse generator network. a Architecture of the pulse-generating network. b Equivalent three nodes feedforward network

Fig. 6

Pulse generator network simulation. a Time response of pulse generator network to an input signal with intensity S ₁=470 nM and duration 50 min (k ₁=5 nM/min, k ₁₂=20 nM/min, λ ₂=0.01 nM/min, λ=0.04 nM/min, K ₁=1 nM, K ₂=100 nM, and n ₁=n ₂=3). b 100 realizations of the pdf of the Y area; c 100 realizations of the pdf of the Y maximum. d 100 realizations of the pdf of the time to maximum of Y

Fig. 7

Moment Independent Robustness Indicator (MIRI) for the Y signal area. a Single realization. b Box plot for 100 realizations

Fig. 8

Conditional robustness for Y area (N=10000). a Probability density function. b Simulation examples conditioning parameters as shown in first row of Table 1

Fig. 9

Multiobjective conditional robustness for area, time to maximum and amplification of Y (N=10000 and parameters values are shown in the forth row of Table 1). a Pdf for time to maximum of Y. b Pdf for area of Y. c Pdf for Intensity of Y. d Simulations example with fixed k ₁₂, K ₂ and λ

Fig. 10

The EGFR-IGF1R pathways in NSCLC. a Pathways graph as presented in [46]. b State variables representation of the EGFR-IGF1R pathways

Fig. 11

Moment Independent Robustness Indicator (MIRI) for ERK activity in EGFR-IGF1R model. a Single realization. b Box plot for 100 realizations

Fig. 12

a Unconditional distribution of evaluation function E R K ^∗. b Conditional robustness for ERK activity (N=10000). c E R K ^∗ time simulation: wild type (black line) vs simulation at conditioned value as in Table 1

Fig. 13

a Unconditional E R K ^∗ activity at EGFR and I G F1R initial condition wild type and at perturbed EGFR and I G F1R. b MIRI of the parameters for 100 realizations. c Effect of conditioning of p ₂₃, p ₂₄,p ₃₅, p ₃₆ and p ₂₇