Interactive Volumetry Of Liver Ablation Zones
- PMID: 26482818
- PMCID: PMC4612735
- DOI: 10.1038/srep15373
Interactive Volumetry Of Liver Ablation Zones
Abstract
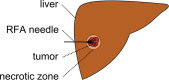
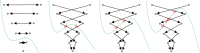
Percutaneous radiofrequency ablation (RFA) is a minimally invasive technique that destroys cancer cells by heat. The heat results from focusing energy in the radiofrequency spectrum through a needle. Amongst others, this can enable the treatment of patients who are not eligible for an open surgery. However, the possibility of recurrent liver cancer due to incomplete ablation of the tumor makes post-interventional monitoring via regular follow-up scans mandatory. These scans have to be carefully inspected for any conspicuousness. Within this study, the RF ablation zones from twelve post-interventional CT acquisitions have been segmented semi-automatically to support the visual inspection. An interactive, graph-based contouring approach, which prefers spherically shaped regions, has been applied. For the quantitative and qualitative analysis of the algorithm's results, manual slice-by-slice segmentations produced by clinical experts have been used as the gold standard (which have also been compared among each other). As evaluation metric for the statistical validation, the Dice Similarity Coefficient (DSC) has been calculated. The results show that the proposed tool provides lesion segmentation with sufficient accuracy much faster than manual segmentation. The visual feedback and interactivity make the proposed tool well suitable for the clinical workflow.
Figures

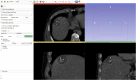
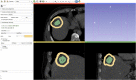

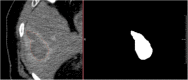


References
-
- Graf D. et al. Multimodal treatment of hepatocellular carcinoma. Eur. J. Intern. Med. 25, 430–437 (2014). - PubMed
-
- Lu D. S. et al. Percutaneous radiofrequency ablation of hepatocellular carcinoma as a bridge to liver transplantation. Hepatology 41, 1130–1137 (2005). - PubMed
-
- Buscarini E. et al. Radiofrequency thermal ablation of liver tumors. Eur. Radiol. 15, 884–894 (2005). - PubMed
-
- Wong S. L. et al. American Society of Clinical Oncology 2009 clinical evidence review on radiofrequency ablation of hepatic metastases from colorectal cancer. J. Clin. Oncol. 28, 493–508 (2010). - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Molecular Biology Databases
Research Materials

