Activation of the intermediate sum in intentional and automatic calculations

Abstract

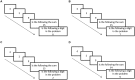
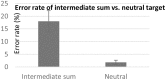
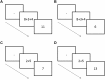
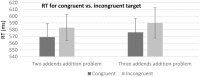
Most research investigating how the cognitive system deals with arithmetic has focused on the processing of two addends. Arithmetic that involves more addends has specific cognitive demands such as the need to compute and hold the intermediate sum. This study examines the intermediate sums activations in intentional and automatic calculations. Experiment 1 included addition problems containing three operands. Participants were asked to calculate the sum and to remember the digits that appeared in the problem. The results revealed an interference effect in which it was hard to identify that the digit representing the intermediate sum was not actually one of the operands. Experiment 2, further examined if the intermediate sum is activated automatically when a task does not require calculation. Here, participants were presented with a prime of an addition problem followed by a target number. The task was to determine whether the target number is odd or even, while ignoring the addition problem in the prime. The results suggested that the intermediate sum of the addition problem in the prime was activated automatically and facilitated the target. Overall, the implications of those findings in the context of theories that relate to cognitive mathematical calculation is further discussed.

Keywords: addition problems; arithmetic problems; automaticity and control; inhibition; intermediate sum; numerical cognition.

FIGURE 1

A schematic representation of the experimental paradigm along with the various conditions are displayed. Three addends are presented one after the other and are followed by two tasks. The first task is to identify whether a specified number is the sum of the addends. The second task is to identify whether a specified digit is one of the addends of the problem. (A) Condition 1 (the absent digit is the intermediate sum). Task a: correct response: “yes,” Task b: correct response: “no.” Note that in this condition the intermediate sum (6) is the digit that one needs to identity as NOT one of the addends. (B) Condition 2 (the absent digit is a neutral digit). Task a: correct response: “yes,” Task b: correct response: “no.”. Note that in this condition a neutral digit (7) is the digit that one needs to identity as not one of the addends. (C) A filler condition. Task a: correct response: “yes,” Task b: correct response: “yes.” (D) A filler condition. Task a: correct response: “no,” Task b: correct response: “yes.”

FIGURE 2

Mean response time (RT) for rejecting a digit representing the intermediate sum versus a neutral digit. Error bars represent standard error mean.

FIGURE 3

Mean error rate for rejecting a digit representing the intermediate sum versus a neutral digit. Error bars represent standard error mean.

FIGURE 4

Schematic representations of the experimental paradigm along with the various conditions are displayed. An addition task of two or three addends is presented for 150 ms followed by a target number. The task is to determine whether the target number is odd or even, while ignoring the arithmetic addition problem. (A) The intermediate sum of two addends in a prime of a three addend problem is congruent with the target. Correct response: “odd” (B) The intermediate sum of two addends in a prime of a three addend problem is incongruent with the target. Correct response: “even.” (C) The sum of two addends in a prime of a two addend problem is congruent with the target. Correct response: “odd.” (D) The sum of two addends in a prime of a two addend problem is incongruent with the target. Correct response: “odd.”

FIGURE 5

Mean RT as a function of the different experimental conditions. Error bars represent standard error mean.