Evolution of the dense packings of spherotetrahedral particles: from ideal tetrahedra to spheres
- PMID: 26490670
- PMCID: PMC4614866
- DOI: 10.1038/srep15640
Evolution of the dense packings of spherotetrahedral particles: from ideal tetrahedra to spheres
Abstract
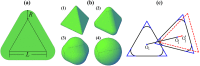
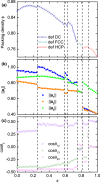
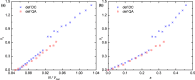
Particle shape plays a crucial role in determining packing characteristics. Real particles in nature usually have rounded corners. In this work, we systematically investigate the rounded corner effect on the dense packings of spherotetrahedral particles. The evolution of dense packing structure as the particle shape continuously deforms from a regular tetrahedron to a sphere is investigated, starting both from the regular tetrahedron and the sphere packings. The dimer crystal and the quasicrystal approximant are used as initial configurations, as well as the two densest sphere packing structures. We characterize the evolution of spherotetrahedron packings from the ideal tetrahedron (s = 0) to the sphere (s = 1) via a single roundness parameter s. The evolution can be partitioned into seven regions according to the shape variation of the packing unit cell. Interestingly, a peak of the packing density Φ is first observed at s ≈ 0.16 in the Φ-s curves where the tetrahedra have small rounded corners. The maximum density of the deformed quasicrystal approximant family (Φ ≈ 0.8763) is slightly larger than that of the deformed dimer crystal family (Φ ≈ 0.8704), and both of them exceed the densest known packing of ideal tetrahedra (Φ ≈ 0.8563).
Figures


References
-
- Zallen R. The Physics of Amorphous Solids (Wiley, New York, 1983).
-
- Torquato S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties (Springer, New York, 2002).
-
- Chaikin P. M. & Lubensky T. C. Principles of Condensed Matter Physics (Cambridge University Press, New York, 2000).
-
- Edwards S. F. in Granular Matter (eds. Mehta A.) 121–140 (Springer, New York, 1994).
-
- Aste T. & Weaire D. The Pursuit of Perfect Packing 2nd edition (Taylor & Francis, Boca Raton, Fla., 2008).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

