A Design Pattern for Decentralised Decision Making
- PMID: 26496359
- PMCID: PMC4619747
- DOI: 10.1371/journal.pone.0140950
A Design Pattern for Decentralised Decision Making
Abstract
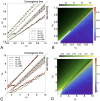
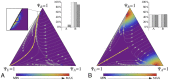
The engineering of large-scale decentralised systems requires sound methodologies to guarantee the attainment of the desired macroscopic system-level behaviour given the microscopic individual-level implementation. While a general-purpose methodology is currently out of reach, specific solutions can be given to broad classes of problems by means of well-conceived design patterns. We propose a design pattern for collective decision making grounded on experimental/theoretical studies of the nest-site selection behaviour observed in honeybee swarms (Apis mellifera). The way in which honeybee swarms arrive at consensus is fairly well-understood at the macroscopic level. We provide formal guidelines for the microscopic implementation of collective decisions to quantitatively match the macroscopic predictions. We discuss implementation strategies based on both homogeneous and heterogeneous multiagent systems, and we provide means to deal with spatial and topological factors that have a bearing on the micro-macro link. Finally, we exploit the design pattern in two case studies that showcase the viability of the approach. Besides engineering, such a design pattern can prove useful for a deeper understanding of decision making in natural systems thanks to the inclusion of individual heterogeneities and spatial factors, which are often disregarded in theoretical modelling.
Conflict of interest statement
Figures
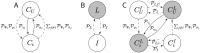
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

