Estimating Relatedness in the Presence of Null Alleles

Abstract

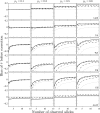
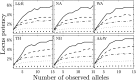
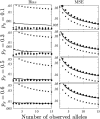
Studies of genetics and ecology often require estimates of relatedness coefficients based on genetic marker data. However, with the presence of null alleles, an observed genotype can represent one of several possible true genotypes. This results in biased estimates of relatedness. As the numbers of marker loci are often limited, loci with null alleles cannot be abandoned without substantial loss of statistical power. Here, we show how loci with null alleles can be incorporated into six estimators of relatedness (two novel). We evaluate the performance of various estimators before and after correction for null alleles. If the frequency of a null allele is <0.1, some estimators can be used directly without adjustment; if it is >0.5, the potency of estimation is too low and such a locus should be excluded. We make available a software package entitled PolyRelatedness v1.6, which enables researchers to optimize these estimators to best fit a particular data set.

Keywords: maximum likelihood; method-of-moment; null alleles; relatedness coefficient.

Figure 1

Modes of identity-by-descent between two diploids. In each plot, the two top circles represent the two alleles in one individual, whereas the bottom circles represent the alleles in the second individual. The lines indicate alleles that are identical-by-descent.

Figure 2

Bias of $\widehat{r}$ before correction as a function of the number of visible alleles at loci with triangular distributed allele frequency. The data that have null alleles with a frequency of 0.1, 0.3, 0.5, or 0.6 are shown in the first to fourth columns. The six estimators compared are as follows: Lynch and Ritland (1999) (L&R), novel estimator A (NA), Wang (2002) (WA), Thomas (2010) (TH), novel estimator B (NB), and the Anderson and Weir (2007) estimator (A&W). Results were obtained from 6 million pairs for four relationships by Monte Carlo simulations except the A&W estimator, including parent–offspring (“—”), full sibs (“– –”), half sibs (“–⋅”), and nonrelatives (“⋯”).

Figure 3

Bias of $\widehat{r}$ after correction as a function of the number of alleles at loci with a triangular allele frequency distribution. Four levels of null allele frequency are shown in each column. Six estimators are compared, as shown in Figure 2. Results were obtained from 60 million pairs for four relationships by Monte Carlo simulations except the A&W estimator, including parent-offspring (“—”), full-sibs (“––”), half-sibs (“–⋅”) and nonrelatives (“⋯”).

Figure 4

The minimum number of loci by using multiple loci to reach $\mathrm{MSE}\left(\widehat{r}\right)<0.01$ for the four relationships shown in Figure 2. The six estimators are the same as in Figure 1. For each estimator, four frequencies of null alleles were simulated: 0.1 (—), 0.3 (– –), 0.5 (–⋅–), 0.6 (⋯), and 0.7 ($•\hspace{0.17em}•\hspace{0.17em}•$), and the observed allele frequency follows the triangular distribution. Results were obtained from 1 million Monte Carlo simulations.

Figure 5

The bias and MSE of $\widehat{r}$ estimated from 20 loci with a triangular allele frequency distribution. Ten million dyads were simulated, with nonrelatives, half sibs, full sibs, and parent–offspring contributing to 70%, 10%, 10%, and 10% of dyads, respectively. The frequency of null alleles was simulated at four levels ($p_y=0.1$, 0.3, 0.5, and 0.6), with each row showing a single level. The results of six estimators are compared: L&R (—), NA (– –), WA (∇), TH (Δ), NA (∘), and A&W (×).