Collective action problem in heterogeneous groups
- PMID: 26503689
- PMCID: PMC4633852
- DOI: 10.1098/rstb.2015.0016
Collective action problem in heterogeneous groups
Abstract
I review the theoretical and experimental literature on the collective action problem in groups whose members differ in various characteristics affecting individual costs, benefits and preferences in collective actions. I focus on evolutionary models that predict how individual efforts and fitnesses, group efforts and the amount of produced collective goods depend on the group's size and heterogeneity, as well as on the benefit and cost functions and parameters. I consider collective actions that aim to overcome the challenges from nature or win competition with neighbouring groups of co-specifics. I show that the largest contributors towards production of collective goods will typically be group members with the highest stake in it or for whom the effort is least costly, or those who have the largest capability or initial endowment. Under some conditions, such group members end up with smaller net pay-offs than the rest of the group. That is, they effectively behave as altruists. With weak nonlinearity in benefit and cost functions, the group effort typically decreases with group size and increases with within-group heterogeneity. With strong nonlinearity in benefit and cost functions, these patterns are reversed. I discuss the implications of theoretical results for animal behaviour, human origins and psychology.
Keywords: altruism; collaboration; cooperation; evolutionarily stable strategies; mathematical modelling.
© 2015 The Author(s).
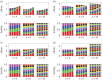
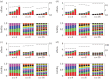
Figures
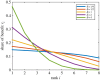
 (Online version in colour.)
(Online version in colour.)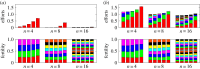
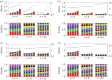
 ). (Online version in colour.)
). (Online version in colour.)
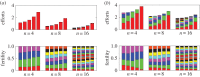
References
-
- Trivers R. 1985. Social evolution. Menlo Park, CA: Benjamin/Cummings.
-
- Jens Krause GDR. 2002. Living in groups. Oxford, UK: Oxford University Press.
-
- Majolo B, Vizioli ADB, Schino G. 2008. Costs and benefits of group living in primates: group size effects on behaviour and demography. Anim. Behav. 76, 1235–1247. (10.1016/j.anbehav.2008.06.008) - DOI
-
- Tucker A. 1950. A two-person dilemma. In Readings in games and information (ed. Rasmussen E.), pp. 7–8. Oxford, UK: Blackwell, 2011.
-
- Olson M. 1965. Logic of collective action: public goods and the theory of groups. Cambridge, MA: Harvard University Press.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
