Relaxation of Loaded ESCRT-III Spiral Springs Drives Membrane Deformation
- PMID: 26522593
- PMCID: PMC4644223
- DOI: 10.1016/j.cell.2015.10.017
Relaxation of Loaded ESCRT-III Spiral Springs Drives Membrane Deformation
Abstract
ESCRT-III is required for lipid membrane remodeling in many cellular processes, from abscission to viral budding and multi-vesicular body biogenesis. However, how ESCRT-III polymerization generates membrane curvature remains debated. Here, we show that Snf7, the main component of ESCRT-III, polymerizes into spirals at the surface of lipid bilayers. When covering the entire membrane surface, these spirals stopped growing when densely packed: they had a polygonal shape, suggesting that lateral compression could deform them. We reasoned that Snf7 spirals could function as spiral springs. By measuring the polymerization energy and the rigidity of Snf7 filaments, we showed that they were deformed while growing in a confined area. Furthermore, we observed that the elastic expansion of compressed Snf7 spirals generated an area difference between the two sides of the membrane and thus curvature. This spring-like activity underlies the driving force by which ESCRT-III could mediate membrane deformation and fission.
Copyright © 2015 The Authors. Published by Elsevier Inc. All rights reserved.
Figures




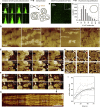
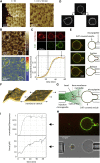
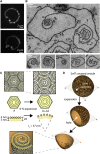
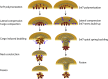





Comment in
-
ESCRT Filaments as Spiral Springs.Dev Cell. 2015 Nov 23;35(4):397-8. doi: 10.1016/j.devcel.2015.11.007. Dev Cell. 2015. PMID: 26609952
References
-
- Babst M., Katzmann D.J., Estepa-Sabal E.J., Meerloo T., Emr S.D. Escrt-III: an endosome-associated heterooligomeric protein complex required for mvb sorting. Dev. Cell. 2002;3:271–282. - PubMed
-
- Bissig C., Gruenberg J. ALIX and the multivesicular endosome: ALIX in Wonderland. Trends Cell Biol. 2014;24:19–25. - PubMed
-
- Buchkovich N.J., Henne W.M., Tang S., Emr S.D. Essential N-terminal insertion motif anchors the ESCRT-III filament during MVB vesicle formation. Dev. Cell. 2013;27:201–214. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Research Materials

