Remote control of self-assembled microswimmers
- PMID: 26538006
- PMCID: PMC4633596
- DOI: 10.1038/srep16035
Remote control of self-assembled microswimmers
Abstract
Physics governing the locomotion of microorganisms and other microsystems is dominated by viscous damping. An effective swimming strategy involves the non-reciprocal and periodic deformations of the considered body. Here, we show that a magnetocapillary-driven self-assembly, composed of three soft ferromagnetic beads, is able to swim along a liquid-air interface when powered by an external magnetic field. More importantly, we demonstrate that trajectories can be fully controlled, opening ways to explore low Reynolds number swimming. This magnetocapillary system spontaneously forms by self-assembly, allowing miniaturization and other possible applications such as cargo transport or solvent flows.
Figures
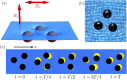


 , allows us to follow various paths such as U-turn, corner and loops. Laid next to one another, the three letters of “ULg” are then obtained. Bead centers are tracked for drawing the triangles at each period, emphasizing the orientation of the structure. The colors indicate the time evolution of each trajectory from dark to red.
, allows us to follow various paths such as U-turn, corner and loops. Laid next to one another, the three letters of “ULg” are then obtained. Bead centers are tracked for drawing the triangles at each period, emphasizing the orientation of the structure. The colors indicate the time evolution of each trajectory from dark to red.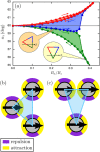
 and ∇ states. (b) Sketch of the platy-isosceles (
and ∇ states. (b) Sketch of the platy-isosceles ( ) configuration. Arrows indicate the horizontal components of the dipoles. Colors indicate whether a pair of dipoles attract or repel compared to zero horizontal field, which depends on their relative orientation. (c) Sketch of the lepto-isosceles (∇) configuration.
) configuration. Arrows indicate the horizontal components of the dipoles. Colors indicate whether a pair of dipoles attract or repel compared to zero horizontal field, which depends on their relative orientation. (c) Sketch of the lepto-isosceles (∇) configuration.
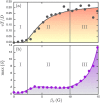
 and ∇ isosceles. (b) The angle θ of the whole structure during three periods. Oscillations are seen evidencing the successive switches. (c) This sketch shows the isosceles states as a function of θ forming a loop at each cycle, i.e. a non-reciprocal motion.
and ∇ isosceles. (b) The angle θ of the whole structure during three periods. Oscillations are seen evidencing the successive switches. (c) This sketch shows the isosceles states as a function of θ forming a loop at each cycle, i.e. a non-reciprocal motion.References
-
- Purcell E. M. Life at low Reynolds number. Am. J. Phys. 45, 3–11 (1977).
-
- Lauga E. Life around the scallop theorem review. Soft Matter 7, 3060–3065 (2011).
-
- Lauga E. & Powers T. R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601 (2009).
-
- Dreyfus R. et al. Microscopic artificial swimmers. Nature 436, 862–865 (2005). - PubMed
-
- Snezhko A. & Aranson I. S. Magnetic manipulation of self-assembled colloidal asters. Nature Mat. 10, 698–703 (2011). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

