Testing for Basins of Wada
- PMID: 26553444
- PMCID: PMC4639726
- DOI: 10.1038/srep16579
Testing for Basins of Wada
Abstract
Nonlinear systems often give rise to fractal boundaries in phase space, hindering predictability. When a single boundary separates three or more different basins of attraction, we say that the set of basins has the Wada property and initial conditions near that boundary are even more unpredictable. Many physical systems of interest with this topological property appear in the literature. However, so far the only approach to study Wada basins has been restricted to two-dimensional phase spaces. Here we report a simple algorithm whose purpose is to look for the Wada property in a given dynamical system. Another benefit of this procedure is the possibility to classify and study intermediate situations known as partially Wada boundaries.
Figures


 . (b) All 1000 × 1000 boxes are labeled either in the interior (white) or in the boundary of the three basins (black). (c) Histogram showing the number of points N that take q steps to be classified as boundary of three. (d) After a maximum, there is an exponential decay of the computational effort related to the fractal structure of the basins. The log-plot reflects this tendency.
. (b) All 1000 × 1000 boxes are labeled either in the interior (white) or in the boundary of the three basins (black). (c) Histogram showing the number of points N that take q steps to be classified as boundary of three. (d) After a maximum, there is an exponential decay of the computational effort related to the fractal structure of the basins. The log-plot reflects this tendency.
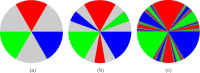
 shows eight basins of attraction mixed intricately. (b) Some boxes are classified to be in the boundary of eight basins (black dots), but not all of them (red dots), which is a clear example of partial Wada. (c) The computational effort presents the usual shape for the Wada boundary, but the points which are not Wada keep refining indefinitely (bar at rightmost). Our algorithm works best in systems with the Wada property. (d) Evolution of the proportion of boxes in the Wada boundary (W8 in black) and proportion of boxes in a boundary which is not Wada (W2−7) as a function of the q-step. The convergence of W8 is used to determine the stopping rule.
shows eight basins of attraction mixed intricately. (b) Some boxes are classified to be in the boundary of eight basins (black dots), but not all of them (red dots), which is a clear example of partial Wada. (c) The computational effort presents the usual shape for the Wada boundary, but the points which are not Wada keep refining indefinitely (bar at rightmost). Our algorithm works best in systems with the Wada property. (d) Evolution of the proportion of boxes in the Wada boundary (W8 in black) and proportion of boxes in a boundary which is not Wada (W2−7) as a function of the q-step. The convergence of W8 is used to determine the stopping rule.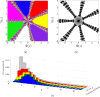
 with r = 7 has seven basins of attraction with the disconnected Wada property. (b) All the boxes lie in the boundary of the seven basins or in the interior. (c) Computational effort as we vary r from 3 to 7. As the number of basins increases the maximum of the histograms shift to the right, that is, the more basins the larger the computational effort. The maximum number of steps q needed for any of these basins to be considered Wada is 21.
with r = 7 has seven basins of attraction with the disconnected Wada property. (b) All the boxes lie in the boundary of the seven basins or in the interior. (c) Computational effort as we vary r from 3 to 7. As the number of basins increases the maximum of the histograms shift to the right, that is, the more basins the larger the computational effort. The maximum number of steps q needed for any of these basins to be considered Wada is 21.References
-
- Nusse H. E., Ott E. & Yorke J. A. Saddle-node bifurcations on fractal basin boundaries. Phys. Rev. Lett. 75(13), 2482–2485 (1995). - PubMed
-
- Portela J. S. E., Caldas I. L., Viana R. L. & Sanjuán M. A. F. Fractal and Wada exit basin boundaries in tokamaks. Int. J. Bifurc. Chaos 17(11), 4067–4079 (2007).
-
- Toroczkai Z., Károlyi G., Péntek Á., Tél T., Grebogi C. & Yorke J. A. Wada dye boundaries in open hydrodynamical flows. Physica A 239(1), 235–243 (1997).
-
- Aguirre J. & Sanjuán M. A. F. Unpredictable behavior in the Duffing oscillator: Wada basins. Phys. D 171(1), 41–51 (2002).
-
- Aguirre J., Vallejo J. C. & Sanjuán M. A. F. Wada basins and chaotic invariant sets in the Hénon-Heiles system. Phys. Rev. E 64(6), 66208 (2001). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

