Using Cox cluster processes to model latent pulse location patterns in hormone concentration data
- PMID: 26553914
- PMCID: PMC5006117
- DOI: 10.1093/biostatistics/kxv046
Using Cox cluster processes to model latent pulse location patterns in hormone concentration data
Abstract
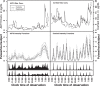
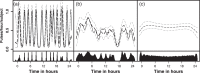
Many hormones, including stress hormones, are intermittently secreted as pulses. The pulsatile location process, describing times when pulses occur, is a regulator of the entire stress system. Characterizing the pulse location process is particularly difficult because the pulse locations are latent; only hormone concentration at sampled times is observed. In addition, for stress hormones the process may change both over the day and relative to common external stimuli. This potentially results in clustering in pulse locations across subjects. Current approaches to characterizing the pulse location process do not capture subject-to-subject clustering in locations. Here we show how a Bayesian Cox cluster process may be adapted as a model of the pulse location process. We show that this novel model of pulse locations is capable of detecting circadian rhythms in pulse locations, clustering of pulse locations between subjects, and identifying exogenous controllers of pulse events. We integrate our pulse location process into a model of hormone concentration, the observed data. A spatial birth-and-death Markov chain Monte Carlo algorithm is used for estimation. We exhibit the strengths of this model on simulated data and adrenocorticotropic and cortisol data collected to study the stress axis in depressed and non-depressed women.
Keywords: Bayesian analysis; Deconvolution; Mixture models; Point processes; Pulsatile hormones.
© The Author 2015. Published by Oxford University Press. All rights reserved. For permissions, please e-mail: journals.permissions@oup.com.
Figures
References
-
- Anderson K. W., O'Sullivan F. (1993). A point process approach to pulsatile hormone data. Presented at the ASA meeting, San Fransisco.
-
- Carroll B. J., Curtis G. C., Mendels J. (1976). Neuroendocrine regulation in depression I. Limbic system-adrenocortical dysfunction. Archives of General Psychiatry 33, 1039–1044. - PubMed
-
- Cox D. R. (1955). Some statistical models related with series of events. Journal of the Royal Statistical Society, Series B 17, 129–164.
-
- Cox D. R., Isham V. (1984) Point Processes. London: Chapman and Hall/CRC.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

