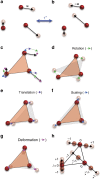
The antisymmetry of distortions
- PMID: 26572582
- PMCID: PMC4660051
- DOI: 10.1038/ncomms9818
The antisymmetry of distortions
Abstract
Distortions are ubiquitous in nature. Under perturbations such as stresses, fields or other changes, a physical system reconfigures by following a path from one state to another; this path, often a collection of atomic trajectories, describes a distortion. Here we introduce an antisymmetry operation called distortion reversal that reverses a distortion pathway. The symmetry of a distortion pathway is then uniquely defined by a distortion group; it has the same form as a magnetic group that involves time reversal. Given its isomorphism to magnetic groups, distortion groups could have a commensurate impact in the study of distortions, as the magnetic groups have had in the study of magnetic structures. Distortion symmetry has important implications for a range of phenomena such as structural and electronic phase transitions, diffusion, molecular conformational changes, vibrations, reaction pathways and interface dynamics.
Figures
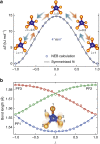

 . The symmetry of this path,
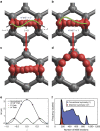
. The symmetry of this path,  , requires that the energy profile in a is symmetric. (b) The superimposed images of β-BaB2O4 along the distortion pathway; their colour varies from orange, through magenta to cyan as λ varies from −1 through 0 to +1. (c) The optical second harmonic generation tensor coefficients along this pathway calculated by Cammarata and Rondinelli (red, green and blue circles) and a polynomial fit (red, green and blue lines) using only the coefficients that are consistent with
, requires that the energy profile in a is symmetric. (b) The superimposed images of β-BaB2O4 along the distortion pathway; their colour varies from orange, through magenta to cyan as λ varies from −1 through 0 to +1. (c) The optical second harmonic generation tensor coefficients along this pathway calculated by Cammarata and Rondinelli (red, green and blue circles) and a polynomial fit (red, green and blue lines) using only the coefficients that are consistent with  point-group symmetry. Distortion symmetry predicts that these coefficients will be odd functions of the distortion parameter, λ, and zero when λ=0.
point-group symmetry. Distortion symmetry predicts that these coefficients will be odd functions of the distortion parameter, λ, and zero when λ=0.
References
-
- Pechukas P. Transition state theory. Annu. Rev. Phys. Chem. 32, 159–177 (1981) .
-
- Bone R. G. A. Deducing the symmetry operations generated at a transition state. Chem. Phys. Lett. 193, 557–564 (1992) .
-
- McIver J. W. & Stanton R. E. Symmetry selection rules for transition states. J. Am. Chem. Soc. 94, 8618–8620 (1972) .
-
- Henkelman G. & Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 113, 9978 (2000) .
-
- Campbell B. J., Stokes H. T., Tanner D. E. & Hatch D. M. ISODISPLACE: a web-based tool for exploring structural distortions. J. Appl. Crystallogr. 39, 607–614 (2006) .
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

