Adaptive Mesh Refinement and Adaptive Time Integration for Electrical Wave Propagation on the Purkinje System

Abstract

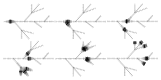
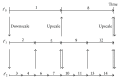
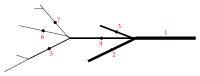
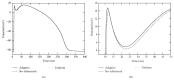
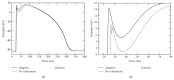
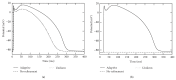
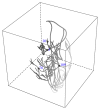
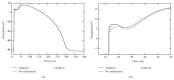
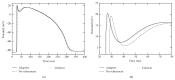
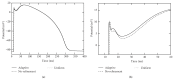
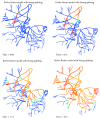
A both space and time adaptive algorithm is presented for simulating electrical wave propagation in the Purkinje system of the heart. The equations governing the distribution of electric potential over the system are solved in time with the method of lines. At each timestep, by an operator splitting technique, the space-dependent but linear diffusion part and the nonlinear but space-independent reactions part in the partial differential equations are integrated separately with implicit schemes, which have better stability and allow larger timesteps than explicit ones. The linear diffusion equation on each edge of the system is spatially discretized with the continuous piecewise linear finite element method. The adaptive algorithm can automatically recognize when and where the electrical wave starts to leave or enter the computational domain due to external current/voltage stimulation, self-excitation, or local change of membrane properties. Numerical examples demonstrating efficiency and accuracy of the adaptive algorithm are presented.

Figure 1

An idealized branch of the Purkinje system.

Figure 2

Adaptively refined grids from a simulation, which use five refinement levels.

Figure 3

Recursive advancing of three mesh refinement levels.

Figure 4

A typical branch in the heart conduction system is highly nonuniform in the sense that the lengths of branch segments, each of which is bounded by two adjacent leaves or branching vertices, may vary significantly. In this figure, branch segments “1” and “4” are not directly connected. Instead, they are connected through a very short branch segment. Similarly, branch segments “4” and “6” are also connected through a very short segment.

Figure 5

Traces of action potentials during the simulation period [0,400] msecs at marked point “4” in the two-dimensional branch shown in Figure 4. The solid curves were from the adaptive simulation. The dotted curves were from the uniform simulation. The dashed curves were from the “no-refinement” simulation. In these simulations, a voltage stimulation is applied from the right side of the radius-variable branch structure. The right plot is a close-up of the left plot.

Figure 6

Traces of action potentials during the simulation period [0,400] msecs at the point marked as “7” in the two-dimensional branch shown in Figure 4. The solid curves were from the adaptive simulation. The dotted curves were from the uniform simulation. The dashed curves were from the “no-refinement” simulation. In these simulations, a voltage stimulation is applied from the right side of the thickness/radius-variable branch structure. The right plot is a close-up of the left plot.

Figure 7

Traces of action potentials during the simulation period [0,400] msecs at marked points “7” and “6” in the two-dimensional branch shown in Figure 4. The solid curves were from the adaptive simulation. The dotted curves were from the uniform simulation. The dashed curves were from the “no-refinement” simulation. In these simulations, a voltage stimulation is applied from the top of the radius-variable branch structure. The left plot corresponds to the marked point “7” and the right plot corresponds to the marked point “6.”

Figure 8

The idealized Purkinje system of the heart.

Figure 9

Traces of action potentials during the simulation period [0,400] msecs at the point marked as “3” in Figure 8. The right plot is a close-up of the left one.

Figure 10

Traces of action potentials during the simulation period [0,400] msecs at the point marked as “20” in Figure 8. The right plot is a close-up of the left one.

Figure 11

Traces of action potentials during the simulation period [0,400] msecs at the point marked as “76” in Figure 8. The right plot is a close-up of the left one.

Figure 12

Traces of action potentials during the simulation period [0,400] msecs at the point marked as “109” in Figure 8. The right plot is a close-up of the left one.

Figure 13

Four plots of the action potential at different times by the AMR-ATI simulation (red denotes activated potential and blue denotes inactivated potential).