Learning of Chunking Sequences in Cognition and Behavior
- PMID: 26584306
- PMCID: PMC4652905
- DOI: 10.1371/journal.pcbi.1004592
Learning of Chunking Sequences in Cognition and Behavior
Abstract
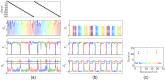
We often learn and recall long sequences in smaller segments, such as a phone number 858 534 22 30 memorized as four segments. Behavioral experiments suggest that humans and some animals employ this strategy of breaking down cognitive or behavioral sequences into chunks in a wide variety of tasks, but the dynamical principles of how this is achieved remains unknown. Here, we study the temporal dynamics of chunking for learning cognitive sequences in a chunking representation using a dynamical model of competing modes arranged to evoke hierarchical Winnerless Competition (WLC) dynamics. Sequential memory is represented as trajectories along a chain of metastable fixed points at each level of the hierarchy, and bistable Hebbian dynamics enables the learning of such trajectories in an unsupervised fashion. Using computer simulations, we demonstrate the learning of a chunking representation of sequences and their robust recall. During learning, the dynamics associates a set of modes to each information-carrying item in the sequence and encodes their relative order. During recall, hierarchical WLC guarantees the robustness of the sequence order when the sequence is not too long. The resulting patterns of activities share several features observed in behavioral experiments, such as the pauses between boundaries of chunks, their size and their duration. Failures in learning chunking sequences provide new insights into the dynamical causes of neurological disorders such as Parkinson's disease and Schizophrenia.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
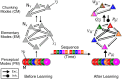





Similar articles
-
Chunking dynamics: heteroclinics in mind.Front Comput Neurosci. 2014 Mar 14;8:22. doi: 10.3389/fncom.2014.00022. eCollection 2014. Front Comput Neurosci. 2014. PMID: 24672469 Free PMC article.
-
How does chunking help working memory?J Exp Psychol Learn Mem Cogn. 2019 Jan;45(1):37-55. doi: 10.1037/xlm0000578. Epub 2018 Apr 26. J Exp Psychol Learn Mem Cogn. 2019. PMID: 29698045
-
The role of chunking in drawing Rey complex figure.Percept Mot Skills. 2015 Apr;120(2):535-55. doi: 10.2466/24.PMS.120v17x6. Epub 2015 Feb 23. Percept Mot Skills. 2015. PMID: 25706345
-
Storage, recall, and novelty detection of sequences by the hippocampus: elaborating on the SOCRATIC model to account for normal and aberrant effects of dopamine.Hippocampus. 2001;11(5):551-68. doi: 10.1002/hipo.1071. Hippocampus. 2001. PMID: 11732708 Review.
-
Learning and production of movement sequences: behavioral, neurophysiological, and modeling perspectives.Hum Mov Sci. 2004 Nov;23(5):699-746. doi: 10.1016/j.humov.2004.10.008. Hum Mov Sci. 2004. PMID: 15589629 Review.
Cited by
-
Interactive reservoir computing for chunking information streams.PLoS Comput Biol. 2018 Oct 8;14(10):e1006400. doi: 10.1371/journal.pcbi.1006400. eCollection 2018 Oct. PLoS Comput Biol. 2018. PMID: 30296262 Free PMC article.
-
Skill in discrete keying sequences is execution rate specific.Psychol Res. 2019 Mar;83(2):235-246. doi: 10.1007/s00426-017-0967-2. Epub 2018 Jan 3. Psychol Res. 2019. PMID: 29299672 Free PMC article.
-
Up to the magical number seven: An evolutionary perspective on the capacity of short term memory.Heliyon. 2021 May 3;7(5):e06955. doi: 10.1016/j.heliyon.2021.e06955. eCollection 2021 May. Heliyon. 2021. PMID: 34013087 Free PMC article. Review.
-
Neuronal Sequence Models for Bayesian Online Inference.Front Artif Intell. 2021 May 21;4:530937. doi: 10.3389/frai.2021.530937. eCollection 2021. Front Artif Intell. 2021. PMID: 34095815 Free PMC article. Review.
-
Planning and navigation as active inference.Biol Cybern. 2018 Aug;112(4):323-343. doi: 10.1007/s00422-018-0753-2. Epub 2018 Mar 23. Biol Cybern. 2018. PMID: 29572721 Free PMC article.
References
-
- Bousfield WA. The occurrence of clustering in the recall of randomly arranged associates. The Journal of General Psychology. 1953;49(2):229–240. 10.1080/00221309.1953.9710088 - DOI

