High-Throughput Single-Cell Kinetics of Virus Infections in the Presence of Defective Interfering Particles

Abstract

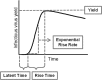
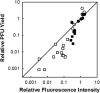
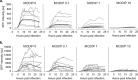
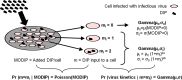
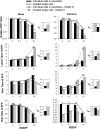
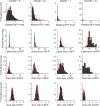
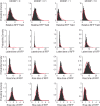
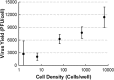
Defective interfering particles (DIPs) are virus mutants that lack essential genes for growth. In coinfections with helper virus, the diversion of viral proteins to the replication and packaging of DIP genomes can interfere with virus production. Mounting cases of DIPs and DIP-like genomes in clinical and natural isolates, as well as growing interest in DIP-based therapies, underscore a need to better elucidate how DIPs work. DIP activity is primarily measured by its inhibition of virus infection yield, an endpoint that masks the dynamic and potentially diverse individual cell behaviors. Using vesicular stomatitis virus (VSV) as a model, we coinfected BHK cells with VSV DIPs and recombinant helper virus carrying a gene encoding a red fluorescent protein (RFP) whose expression correlates with the timing and level of virus release. For single cells within a monolayer, 10 DIPs per cell suppressed the reporter expression in only 1.2% of the cells. In most cells, it slowed and reduced viral gene expression, manifested as a shift in mean latent time from 4 to 6 h and reduced virus yields by 10-fold. For single cells isolated in microwells, DIP effects were more pronounced, reducing virus yields by 100-fold and extending latent times to 12 h, including individual instances above 20 h. Together, these results suggest that direct or indirect cell-cell interactions prevent most coinfected cells from being completely suppressed by DIPs. Finally, a gamma distribution model captures well how the infection kinetics quantitatively depends on the DIP dose. Such models will be useful for advancing a predictive biology of DIP-associated virus growth and infection spread.

Importance: During the last century, basic studies in virology have focused on developing a molecular mechanistic understanding of how infectious viruses reproduce in their living host cells. However, over the last 10 years, the advent of deep sequencing and other powerful technologies has revealed in natural and patient infections that viruses do not act alone. Instead, viruses are often accompanied by defective virus-like particles that carry large deletions in their genomes and fail to replicate on their own. Coinfections of viable and defective viruses behave in unpredictable ways, but they often interfere with normal virus growth, potentially enabling infections to evade host immune surveillance. In the current study, controlled levels of defective viruses are coinfected with viable viruses that have been engineered to express a fluorescent reporter protein during infection. Unique profiles of reporter expression acquired from thousands of coinfected cells reveal how interference acts at multiple stages of infection.

FIG 1

Kinetic parameters of single-cell infection. Measures of a single round of infection within a single cell, taken over time, provide a growth curve, from which characteristic parameters may be extracted. Latent time is the interval between entry of adsorbed virus into its host cell and the initial rise of infectious virus production. Rise time is the interval over which the cell produces virus. Exponential rise rate is estimated by fitting an exponential growth function to infectious virus release (e^{rise rate × time}). Yield is the amount of infectious virus produced from a cell over the course of an infection. Similar kinetic parameters of infection may be defined for measures of viral gene expression (e.g., production of red fluorescent protein [RFP]).

FIG 2

Dependence of virus yields on DIP level. Yields of virus production were measured for cells in a population (gray hexagons; three wells at each multiplicity of DIPs [MODIP]) and for isolated single cells (box plots; 15 to 19 cells at each MODIP). Cells were coinfected with virus (MOI of 30) and defective interfering particles (MODIP), and viral yields were measured at 24 hpi. For cells in a population, standard error bars are smaller than the data point size except for MODIP of 10 (gray error bars). Box plots cover 25 to 75% of single-cell yields, and the bars cover 5 to 95% of single-cell yields. Within each box are lines showing the median (solid) and mean (dashed) of the single-cell yields. Differences between population and single-cell yields are statistically significant (P < 0.05), except at an MODIP of 0.1 (P = 0.065).

FIG 3

Correlation of virus production with reporter expression in single cells. Reporter (RFP) yields correlate with virus (PFU) yields in isolated single cells (r = 0.856; P < 0.01; n = 33). Cells coinfected with virus (MOI of 30) and various DIP levels are indicated by filled circles (MODIP of 0), open circles (MODIP of 0.1), filled squares (MODIP of 1), and open squares (MODIP of 10). Relative RFP and PFU values were determined by normalizing data to their respective average values from infections lacking DIPs (MOI of 30 and MODIP of 0). The parity line (r = 1.00) is shown for reference.

FIG 4

Dependence of RFP reporter expression on DIP levels. RFP reporter expression was tracked in single cells coinfected at an MOI of 30 and various multiplicities of DIPs (MODIP), as indicated. Gray lines show RFP reporter expression trajectories from representative isolated cells in microwells (a) and cells in a population (b). The black line in each plot shows the average RFP trajectory of all tracked cells. RFP intensity is shown in arbitrary units (au).

FIG 5

Effects of DIPs on distributions of infection parameters from single cells. (a and b) Estimated parameters for isolated single cells (n = 458–1,064) (a) and individual cells within a population (n = 2,452–6,056) (b). All cells were coinfected at an MOI of 30 and the DIP levels shown. Each histogram was generated by dividing the measured data range into 30 bins, except for the rise rate distribution from isolated single cells at an MODIP of 10, where the number of cells was lower (n = 16) and the bin number was 5. Parameter distributions at different DIP levels (MODIP of 0, 1, and 10) were different from each other (P < 0.01). (c) Mean and variance are summarized for distributions of infection kinetic parameters, which may be due to the exclusion of nonproducer cells in rise time measurements biasing the observed rise time distributions toward producer cells with lower rise time values.

FIG 6

Dependence of producer cells on DIP level. Cells were coinfected with RFP reporter virus (MOI of 30) and different levels of DIPs. Productive cells were quantified based on the presence of detectable RFP from single cells within a population or based on their ability to form plaques.

FIG 7

Mathematical model of the dependence of viral gene expression kinetics on DIP levels in single cells. Added DIPs (black bullets) adsorb to cells (pink) following a Poisson distribution. For a given number of DIP particles per cell (m), the infection kinetic parameter distributions are modeled by a gamma distribution where the mean (μ) and variance (σ) depend on the DIP input level. Both μ₀ and σ₀ were calculated based on the RFP kinetic parameters measured at an MODIP of 0, and values of μ and σ shifted from an MODIP of 0 depending on the DIP level (m_i = 0,1,2,3..) by power k_a and k_b, respectively. All cells are assumed to be coinfected with viable virus particles at a high and constant MOI. Pr, probability.

FIG 8

Dependence of infection kinetic parameters on DIP levels. The observed changes (bars) and fit values (circles) in the mean (left) and variance (right) of relative yield, latent time, rise time, and rise rate of RFP (ordinate) in isolated single cells (gray bars and circles) and in single cells within a population (black bars and white circles) with increasing MODIP and a fixed MOI of 30 are shown. The insets show the degrees of change in the mean (k_a) and variance (k_b) of infection kinetic parameters in isolated single cells (gray bars) and in single cells within a population (black bars). While the fit values of mean and variance of infection kinetic parameters matched the observed values, the mean of rise time at an MODIP of 10 was higher than the observed value.

FIG 9

Measured and fit distributions of infection kinetic parameters for isolated single cells. Measured probability densities (ordinate) of relative yield, latent time, rise time, and rise rate of RFP (abscissa) are shown as black bars. Red curves represent model estimates of probability densities. Each column belongs to a different MODIP value, as indicated.

FIG 10

Measured and fit distributions of infection kinetic parameters for single cells in a population. Measured probability densities (ordinate) of relative yield, latent time, rise time, and rise rate of RFP (abscissa) are given as black bars. Red curves represent model estimates of probability densities. Each column belongs to a different MODIP value, as indicated.

FIG 11

Effect of cell density on infectious virus yield. Infectious virus production on a per cell basis increases proportionally with the local density of cells. Virus yields at each cell density were measured by plaque assay (n = 10). Error bars represent standard deviation. The highest density (e.g., 10⁴ cells per well) corresponded with nearly 100% confluence.

FIG 12

Correlations between infection kinetic parameters for isolated single cells. Pairs of infection kinetics parameters measured in isolated single cells were compared in each plot. Each data point represents a single cell coinfected at an MOI of 30 with a different MODIP, as indicated by the shading.

FIG 13

Correlations between infection kinetic parameters for single cells in a population. Pairs of infection parameters measured in individual cells in a population were compared in each plot. Each data point represents a single cell coinfected at an MOI of 30 with a different MODIP, as indicated by the shading.