Positron Emission Tomography: Current Challenges and Opportunities for Technological Advances in Clinical and Preclinical Imaging Systems
- PMID: 26643024
- PMCID: PMC5299095
- DOI: 10.1146/annurev-bioeng-071114-040723
Positron Emission Tomography: Current Challenges and Opportunities for Technological Advances in Clinical and Preclinical Imaging Systems
Abstract
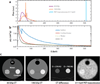
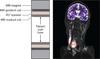
Positron emission tomography (PET) imaging is based on detecting two time-coincident high-energy photons from the emission of a positron-emitting radioisotope. The physics of the emission, and the detection of the coincident photons, give PET imaging unique capabilities for both very high sensitivity and accurate estimation of the in vivo concentration of the radiotracer. PET imaging has been widely adopted as an important clinical modality for oncological, cardiovascular, and neurological applications. PET imaging has also become an important tool in preclinical studies, particularly for investigating murine models of disease and other small-animal models. However, there are several challenges to using PET imaging systems. These include the fundamental trade-offs between resolution and noise, the quantitative accuracy of the measurements, and integration with X-ray computed tomography and magnetic resonance imaging. In this article, we review how researchers and industry are addressing these challenges.
Keywords: PET/CT; PET/MRI; multimodality kinetic modeling; silicon photomultipliers; system model; tomographic image reconstruction.
Figures
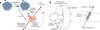








References
-
- Humm JL, Rosenfeld A, Del Guerra A. From PET detectors to PET scanners. Eur. J. Nucl. Med. Mol. Imaging. 2003;30(11):1574–1597. - PubMed
-
- Bacharach SL. Positron emission tomography. In: Dilsizian V, Pohost GM, editors. Cardiac CT, PET and MR. 2nd. Hoboken, NJ: Blackwell; 2010. pp. 3–29.
-
- Van Eijk CWE. Radiation detector developments in medical applications: inorganic scintillators in positron emission tomography. Radiat. Prot. Dosimetry. 2008;129(1–3):13–21. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

