Analytic Models of Oxygen and Nutrient Diffusion, Metabolism Dynamics, and Architecture Optimization in Three-Dimensional Tissue Constructs with Applications and Insights in Cerebral Organoids
- PMID: 26650970
- PMCID: PMC5029285
- DOI: 10.1089/ten.TEC.2015.0375
Analytic Models of Oxygen and Nutrient Diffusion, Metabolism Dynamics, and Architecture Optimization in Three-Dimensional Tissue Constructs with Applications and Insights in Cerebral Organoids
Abstract
Diffusion models are important in tissue engineering as they enable an understanding of gas, nutrient, and signaling molecule delivery to cells in cell cultures and tissue constructs. As three-dimensional (3D) tissue constructs become larger, more intricate, and more clinically applicable, it will be essential to understand internal dynamics and signaling molecule concentrations throughout the tissue and whether cells are receiving appropriate nutrient delivery. Diffusion characteristics present a significant limitation in many engineered tissues, particularly for avascular tissues and for cells whose viability, differentiation, or function are affected by concentrations of oxygen and nutrients. This article seeks to provide novel analytic solutions for certain cases of steady-state and nonsteady-state diffusion and metabolism in basic 3D construct designs (planar, cylindrical, and spherical forms), solutions that would otherwise require mathematical approximations achieved through numerical methods. This model is applied to cerebral organoids, where it is shown that limitations in diffusion and organoid size can be partially overcome by localizing metabolically active cells to an outer layer in a sphere, a regionalization process that is known to occur through neuroglial precursor migration both in organoids and in early brain development. The given prototypical solutions include a review of metabolic information for many cell types and can be broadly applied to many forms of tissue constructs. This work enables researchers to model oxygen and nutrient delivery to cells, predict cell viability, study dynamics of mass transport in 3D tissue constructs, design constructs with improved diffusion capabilities, and accurately control molecular concentrations in tissue constructs that may be used in studying models of development and disease or for conditioning cells to enhance survival after insults like ischemia or implantation into the body, thereby providing a framework for better understanding and exploring the characteristics and behaviors of engineered tissue constructs.
Figures













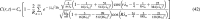

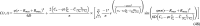
References
-
- Suda T., Takubo K., and Semenza G.L. Metabolic regulation of hematopoietic stem cells in the hypoxic niche. Cell Stem Cell 9, 298, 2011. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
