Intrinsic and realized generation intervals in infectious-disease transmission
- PMID: 26674948
- PMCID: PMC4707754
- DOI: 10.1098/rspb.2015.2026
Intrinsic and realized generation intervals in infectious-disease transmission
Abstract
The generation interval is the interval between the time when an individual is infected by an infector and the time when this infector was infected. Its distribution underpins estimates of the reproductive number and hence informs public health strategies. Empirical generation-interval distributions are often derived from contact-tracing data. But linking observed generation intervals to the underlying generation interval required for modelling purposes is surprisingly not straightforward, and misspecifications can lead to incorrect estimates of the reproductive number, with the potential to misguide interventions to stop or slow an epidemic. Here, we clarify the theoretical framework for three conceptually different generation-interval distributions: the 'intrinsic' one typically used in mathematical models and the 'forward' and 'backward' ones typically observed from contact-tracing data, looking, respectively, forward or backward in time. We explain how the relationship between these distributions changes as an epidemic progresses and discuss how empirical generation-interval data can be used to correctly inform mathematical models.
Keywords: contact-tracing; epidemiological model; generation interval; reproductive number.
© 2015 The Authors.
Figures
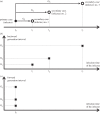


 nE = nI = 3; mean latency and mean infectious duration both equal 5 days; Monte Carlo iterations = 30; population size = 25 000.
nE = nI = 3; mean latency and mean infectious duration both equal 5 days; Monte Carlo iterations = 30; population size = 25 000.

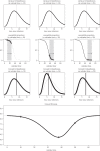
 nE = nI = 3; mean latency and mean infectious duration both equal to 5 days; population size at 25 000. (a) Fit to the mean of the backward generation interval distribution. Solid black circles are the simulated backward generation intervals data. The red solid thick curve is the fitted mean backward generation interval b from the Erlang SEIR model to the mean backward generation intervals data. The red dashed thick curve is the fitted mean backward generation interval b when fitting (naively) the intrinsic distribution g from the same Erlang SEIR model to the backward generation intervals data. The thin grey curve is b when using the ‘true’ parameter values that generated the simulated data. (b) Fit to the variance of the backward generation interval distribution. Open circles represent the simulated data. The red thick solid line is the variance of the fitted distribution b when fitting b to the simulated backward generation intervals data. The red thick dashed line represents the variance of the fitted distribution b when (naively) fitting the intrinsic distribution g to the simulated backward generation intervals data. Only the points to the left of the vertical dashed line (at calendar time 50) were used in both fits. An approximate Bayesian computation method with 1000 iterations was performed for both fits. (Online version in colour.)
nE = nI = 3; mean latency and mean infectious duration both equal to 5 days; population size at 25 000. (a) Fit to the mean of the backward generation interval distribution. Solid black circles are the simulated backward generation intervals data. The red solid thick curve is the fitted mean backward generation interval b from the Erlang SEIR model to the mean backward generation intervals data. The red dashed thick curve is the fitted mean backward generation interval b when fitting (naively) the intrinsic distribution g from the same Erlang SEIR model to the backward generation intervals data. The thin grey curve is b when using the ‘true’ parameter values that generated the simulated data. (b) Fit to the variance of the backward generation interval distribution. Open circles represent the simulated data. The red thick solid line is the variance of the fitted distribution b when fitting b to the simulated backward generation intervals data. The red thick dashed line represents the variance of the fitted distribution b when (naively) fitting the intrinsic distribution g to the simulated backward generation intervals data. Only the points to the left of the vertical dashed line (at calendar time 50) were used in both fits. An approximate Bayesian computation method with 1000 iterations was performed for both fits. (Online version in colour.)References
-
- Anderson RM, May RM. 1991. Infectious diseases of humans: dynamics and control. Oxford, UK: Oxford University Press.
Publication types
MeSH terms
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
