Across population genomic prediction scenarios in which Bayesian variable selection outperforms GBLUP

Abstract

Background: The use of information across populations is an attractive approach to increase the accuracy of genomic prediction for numerically small populations. However, accuracies of across population genomic prediction, in which reference and selection individuals are from different populations, are currently disappointing. It has been shown for within population genomic prediction that Bayesian variable selection models outperform GBLUP models when the number of QTL underlying the trait is low. Therefore, our objective was to identify across population genomic prediction scenarios in which Bayesian variable selection models outperform GBLUP in terms of prediction accuracy. In this study, high density genotype information of 1033 Holstein Friesian, 105 Groningen White Headed, and 147 Meuse-Rhine-Yssel cows were used. Phenotypes were simulated using two changing variables: (1) the number of QTL underlying the trait (3000, 300, 30, 3), and (2) the correlation between allele substitution effects of QTL across populations, i.e. the genetic correlation of the simulated trait between the populations (1.0, 0.8, 0.4).

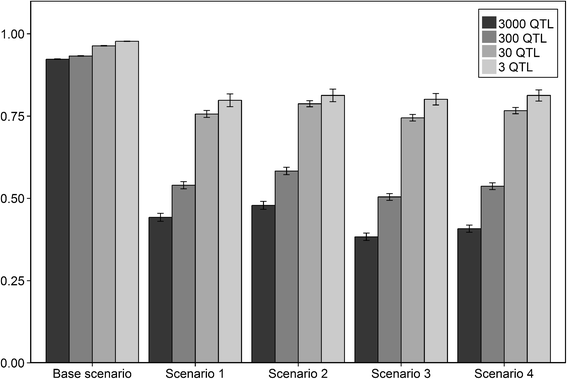
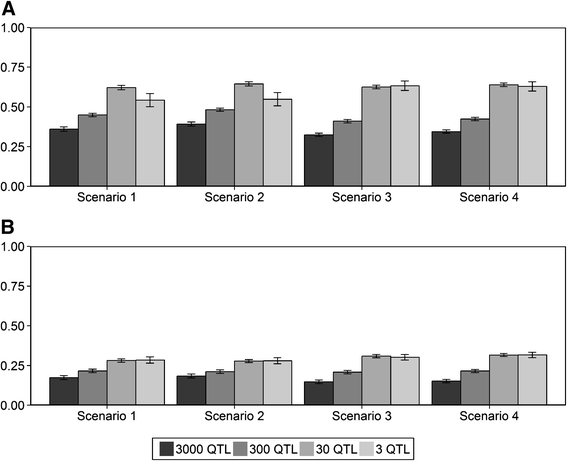
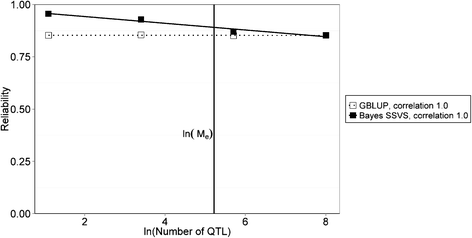
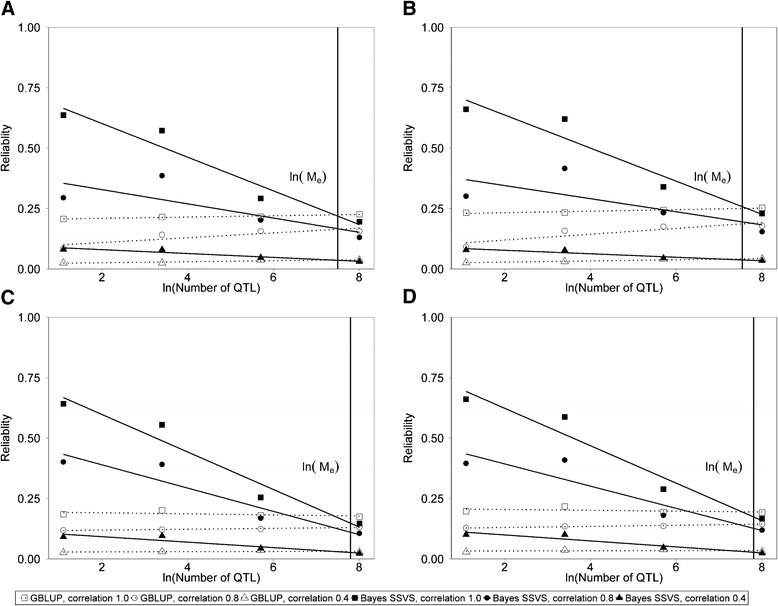
Results: The accuracy obtained by the Bayesian variable selection model was depending on the number of QTL underlying the trait, with a higher accuracy when the number of QTL was lower. This trend was more pronounced for across population genomic prediction than for within population genomic prediction. It was shown that Bayesian variable selection models have an advantage over GBLUP when the number of QTL underlying the simulated trait was small. This advantage disappeared when the number of QTL underlying the simulated trait was large. The point where the accuracy of Bayesian variable selection and GBLUP became similar was approximately the point where the number of QTL was equal to the number of independent chromosome segments (M e ) across the populations.

Conclusion: Bayesian variable selection models outperform GBLUP when the number of QTL underlying the trait is smaller than M e . Across populations, M e is considerably larger than within populations. So, it is more likely to find a number of QTL underlying a trait smaller than M e across populations than within population. Therefore Bayesian variable selection models can help to improve the accuracy of across population genomic prediction.

Fig. 1

Accuracies of genomic prediction assuming equal allele substitution effects across populations. Mean accuracies of genomic prediction (± standard error) obtained by the Bayesian variable selection model assuming equal allele substitution effects across the three populations for five different scenarios; Base scenario: reference = HF, selection candidates = HF; Scenario 1: reference = HF, selection candidates = GWH; Scenario 2: reference = HF & MRY, selection candidates = GWH; Scenario 3: reference = HF, selection candidates = MRY; Scenario 4: reference = HF & GWH, selection candidates = MRY

Fig. 2

Accuracies of genomic prediction assuming different allele substitution effects across populations. Mean accuracies of genomic prediction (± standard error) obtained by the Bayesian variable selection model assuming genetic correlations of a 0.8 or b 0.4 across the three populations for four different scenarios; Scenario 1: reference = HF, selection candidates = GWH; Scenario 2: reference = HF & MRY, selection candidates = GWH; Scenario 3: reference = HF, selection candidates = MRY; Scenario 4: reference = HF & GWH, selection candidates = MRY

Fig. 3

Comparison of the reliability of within population genomic prediction using Bayesian variable selection or GBLUP models. Comparison of the mean reliability of genomic prediction using Bayesian variable selection or GBLUP models for the within population scenario. The vertical line indicates the natural logarithm of the number of independent chromosomes (M _e). M _e is estimated by Wientjes et al. [25] as: $M_e=\frac{1}{Var\left({\mathbf{G}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}-{\mathbf{A}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}\right)}$; where ${\mathbf{G}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}$ refers to the genomic relationship between individual i from population 1 and individual j from population 2, ${\mathbf{A}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}$ refers to the pedigree relationship between individual i from population 1 and individual j from population 2, and the variance is taken over all pair-wise relationships between the individuals in the reference population and the selection candidates

Fig. 4

Comparison of the reliability of across population genomic prediction using Bayesian variable selection or GBLUP models. Comparison of the mean reliability of genomic prediction using Bayesian variable selection or GBLUP models for the four across population scenarios with genetic correlation of 1.0, 0.8 or 0.4 across populations; a Scenario 1: reference = HF, selection candidates = GWH; b Scenario 2: reference = HF & MRY, selection candidates = GWH; c Scenario 3: reference = HF, selection candidates = MRY; d Scenario 4: reference = HF & GWH, selection candidates = MRY. The vertical line indicates the natural logarithm of the number of independent chromosome segments (M _e). M _e is estimated by Wientjes et al. [25] as: $M_e=\frac{1}{Var\left({\mathbf{G}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}-{\mathbf{A}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}\right)}$; where ${\mathbf{G}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}$ refers to the genomic relationship between individual i from population 1 and individual j from population 2, ${\mathbf{A}}_{\mathit{Pop}{.1}_i,\mathit{Pop}{.2}_j}$ refers to the pedigree relationship between individual i from population 1 and individual j from population 2, and the variance is taken over all pair-wise relationships between the individuals in the reference population and the selection candidates